Exact Recovery of Community Detection in dependent Gaussian Mixture Models
Paper and Code
Sep 23, 2022

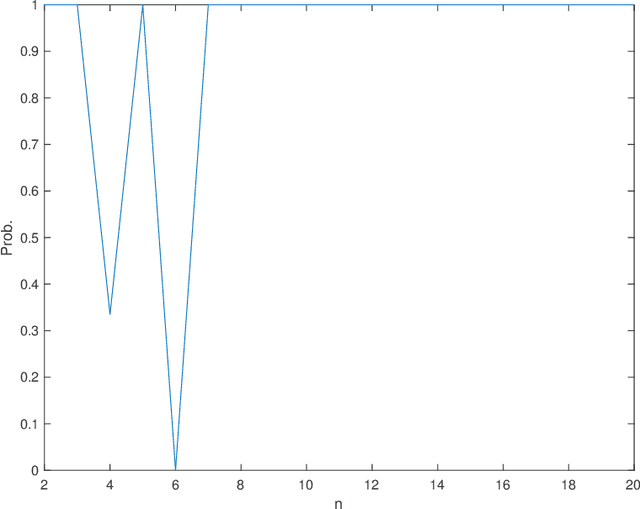
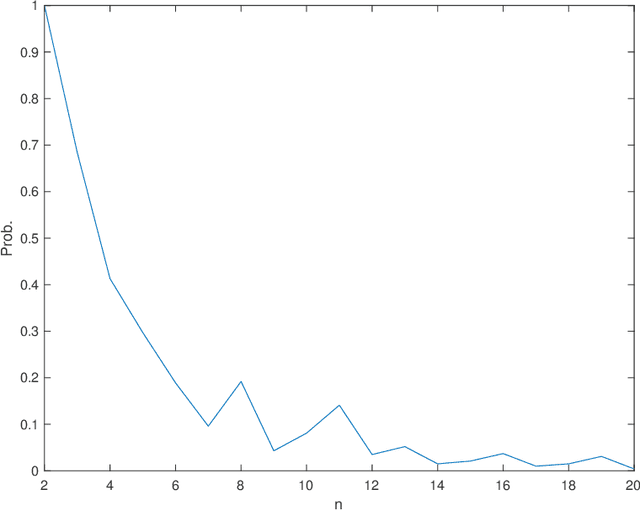
We study the community detection problem on a Gaussian mixture model, in which (1) vertices are divided into $k\geq 2$ distinct communities that are not necessarily equally-sized; (2) the Gaussian perturbations for different entries in the observation matrix are not necessarily independent or identically distributed. We prove necessary and sufficient conditions for the exact recovery of the maximum likelihood estimation (MLE), and discuss the cases when these necessary and sufficient conditions give sharp threshold. Applications include the community detection on a graph where the Gaussian perturbations of observations on each edge is the sum of i.i.d.~Gaussian random variables on its end vertices, in which we explicitly obtain the threshold for the exact recovery of the MLE.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge