Deep generative modelling of canonical ensemble with differentiable thermal properties

We propose a variational modelling method with differentiable temperature for canonical ensembles. Using a deep generative model, the free energy is estimated and minimized simultaneously in a continuous temperature range. At optimal, this generative model is a Boltzmann distribution with temperature dependence. The training process requires no dataset, and works with arbitrary explicit density generative models. We applied our method to study the phase transitions (PT) in the Ising and XY models, and showed that the direct-sampling simulation of our model is as accurate as the Markov Chain Monte Carlo (MCMC) simulation, but more efficient. Moreover, our method can give thermodynamic quantities as differentiable functions of temperature akin to an analytical solution. The free energy aligns closely with the exact one to the second-order derivative, so this inclusion of temperature dependence enables the otherwise biased variational model to capture the subtle thermal effects at the PTs. These findings shed light on the direct simulation of physical systems using deep generative models

Learning Non-linear Wavelet Transformation via Normalizing Flow

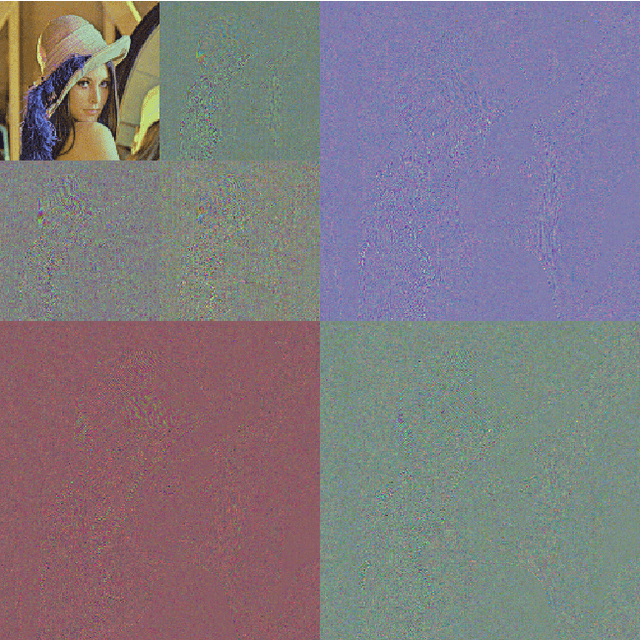
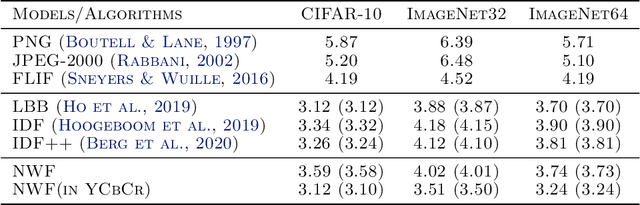
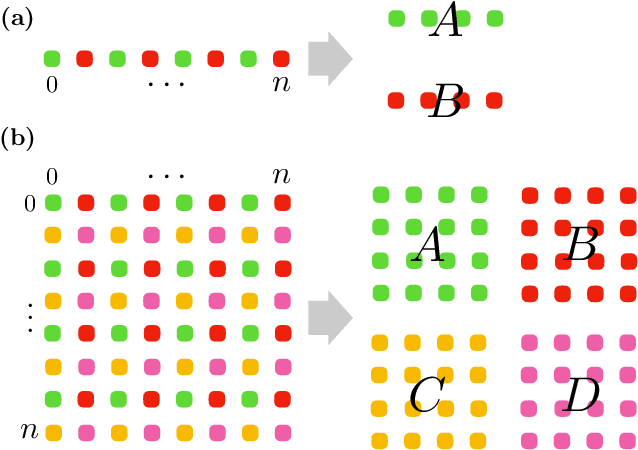
Wavelet transformation stands as a cornerstone in modern data analysis and signal processing. Its mathematical essence is an invertible transformation that discerns slow patterns from fast patterns in the frequency domain, which repeats at each level. Such an invertible transformation can be learned by a designed normalizing flow model. With a factor-out scheme resembling the wavelet downsampling mechanism, a mutually independent prior, and parameter sharing along the depth of the network, one can train normalizing flow models to factor-out variables corresponding to fast patterns at different levels, thus extending linear wavelet transformations to non-linear learnable models. In this paper, a concrete way of building such flows is given. Then, a demonstration of the model's ability in lossless compression task, progressive loading, and super-resolution (upsampling) task. Lastly, an analysis of the learned model in terms of low-pass/high-pass filters is given.

Neural Canonical Transformation with Symplectic Flows

Canonical transformation plays a fundamental role in simplifying and solving classical Hamiltonian systems. We construct flexible and powerful canonical transformations as generative models using symplectic neural networks. The model transforms physical variables towards a latent representation with an independent harmonic oscillator Hamiltonian. Correspondingly, the phase space density of the physical system flows towards a factorized Gaussian distribution in the latent space. Since the canonical transformation preserves the Hamiltonian evolution, the model captures nonlinear collective modes in the learned latent representation. We present an efficient implementation of symplectic neural coordinate transformations and two ways to train the model. The variational free energy calculation is based on the analytical form of physical Hamiltonian. While the phase space density estimation only requires samples in the coordinate space for separable Hamiltonians. We demonstrate appealing features of neural canonical transformation using toy problems including two-dimensional ring potential and harmonic chain. Finally, we apply the approach to real-world problems such as identifying slow collective modes in alanine dipeptide and conceptual compression of the MNIST dataset.

Neural Network Renormalization Group

We present a variational renormalization group (RG) approach using a deep generative model based on normalizing flows. The model performs hierarchical change-of-variables transformations from the physical space to a latent space with reduced mutual information. Conversely, the neural net directly maps independent Gaussian noises to physical configurations following the inverse RG flow. The model has an exact and tractable likelihood, which allows unbiased training and direct access to the renormalized energy function of the latent variables. To train the model, we employ probability density distillation for the bare energy function of the physical problem, in which the training loss provides a variational upper bound of the physical free energy. We demonstrate practical usage of the approach by identifying mutually independent collective variables of the Ising model and performing accelerated hybrid Monte Carlo sampling in the latent space. Lastly, we comment on the connection of the present approach to the wavelet formulation of RG and the modern pursuit of information preserving RG.