Learning Non-linear Wavelet Transformation via Normalizing Flow

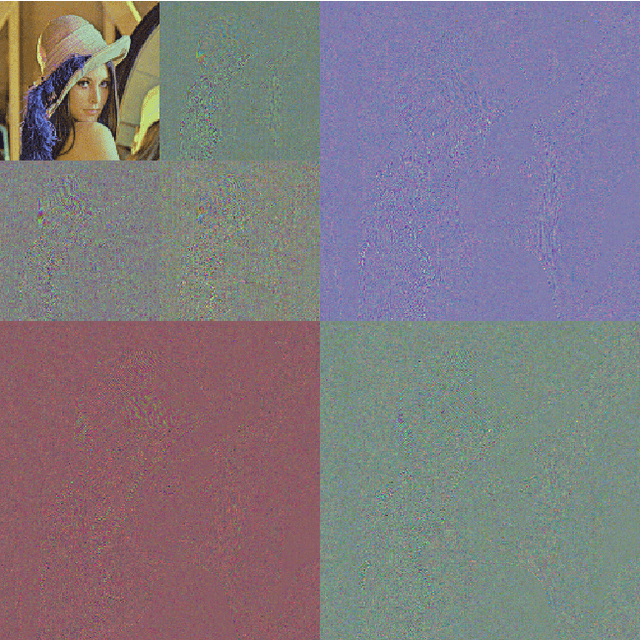
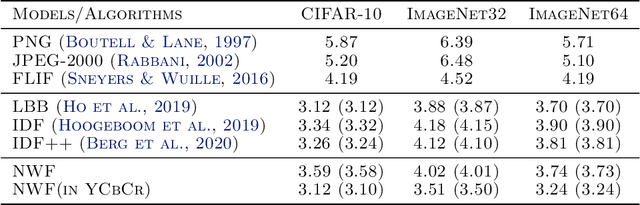
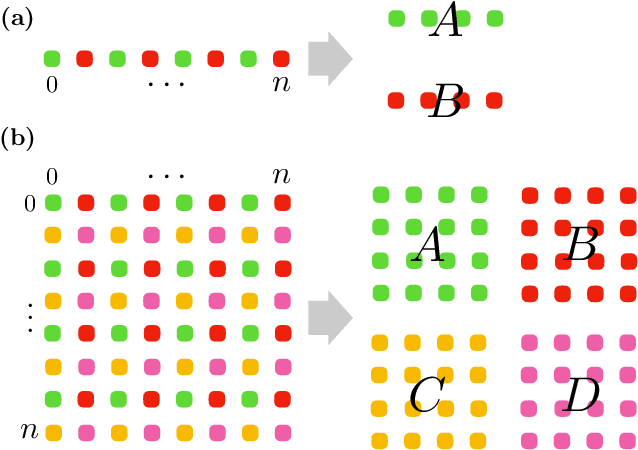
Wavelet transformation stands as a cornerstone in modern data analysis and signal processing. Its mathematical essence is an invertible transformation that discerns slow patterns from fast patterns in the frequency domain, which repeats at each level. Such an invertible transformation can be learned by a designed normalizing flow model. With a factor-out scheme resembling the wavelet downsampling mechanism, a mutually independent prior, and parameter sharing along the depth of the network, one can train normalizing flow models to factor-out variables corresponding to fast patterns at different levels, thus extending linear wavelet transformations to non-linear learnable models. In this paper, a concrete way of building such flows is given. Then, a demonstration of the model's ability in lossless compression task, progressive loading, and super-resolution (upsampling) task. Lastly, an analysis of the learned model in terms of low-pass/high-pass filters is given.