Aggregation of Multi Diffusion Models for Enhancing Learned Representations

Diffusion models have achieved remarkable success in image generation, particularly with the various applications of classifier-free guidance conditional diffusion models. While many diffusion models perform well when controlling for particular aspect among style, character, and interaction, they struggle with fine-grained control due to dataset limitations and intricate model architecture design. This paper introduces a novel algorithm, Aggregation of Multi Diffusion Models (AMDM), which synthesizes features from multiple diffusion models into a specified model, enhancing its learned representations to activate specific features for fine-grained control. AMDM consists of two key components: spherical aggregation and manifold optimization. Spherical aggregation merges intermediate variables from different diffusion models with minimal manifold deviation, while manifold optimization refines these variables to align with the intermediate data manifold, enhancing sampling quality. Experimental results demonstrate that AMDM significantly improves fine-grained control without additional training or inference time, proving its effectiveness. Additionally, it reveals that diffusion models initially focus on features such as position, attributes, and style, with later stages improving generation quality and consistency. AMDM offers a new perspective for tackling the challenges of fine-grained conditional control generation in diffusion models: We can fully utilize existing conditional diffusion models that control specific aspects, or develop new ones, and then aggregate them using the AMDM algorithm. This eliminates the need for constructing complex datasets, designing intricate model architectures, and incurring high training costs. Code is available at: https://github.com/Hammour-steak/AMDM

Image Restoration Through Generalized Ornstein-Uhlenbeck Bridge

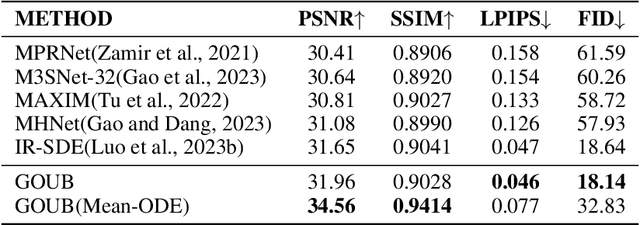
Diffusion models possess powerful generative capabilities enabling the mapping of noise to data using reverse stochastic differential equations. However, in image restoration tasks, the focus is on the mapping relationship from low-quality images to high-quality images. To address this, we introduced the Generalized Ornstein-Uhlenbeck Bridge (GOUB) model. By leveraging the natural mean-reverting property of the generalized OU process and further adjusting the variance of its steady-state distribution through the Doob's h-transform, we achieve diffusion mappings from point to point with minimal cost. This allows for end-to-end training, enabling the recovery of high-quality images from low-quality ones. Additionally, we uncovered the mathematical essence of some bridge models, all of which are special cases of the GOUB and empirically demonstrated the optimality of our proposed models. Furthermore, benefiting from our distinctive parameterization mechanism, we proposed the Mean-ODE model that is better at capturing pixel-level information and structural perceptions. Experimental results show that both models achieved state-of-the-art results in various tasks, including inpainting, deraining, and super-resolution. Code is available at https://github.com/Hammour-steak/GOUB.