Parameter Estimation on Homogeneous Spaces

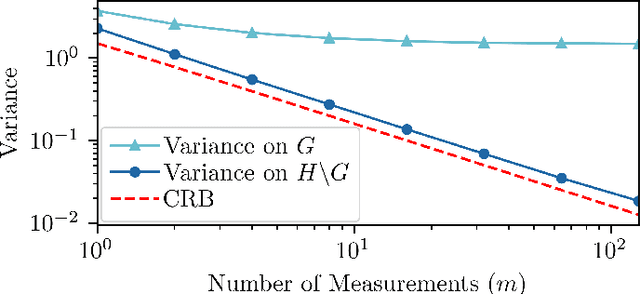
The Fisher Information Metric (FIM) and the associated Cram\'er-Rao Bound (CRB) are fundamental tools in statistical signal processing, which inform the efficient design of experiments and algorithms for estimating the underlying parameters. In this article, we investigate these concepts for the case where the parameters lie on a homogeneous space. Unlike the existing Fisher-Rao theory for general Riemannian manifolds, our focus is to leverage the group-theoretic structure of homogeneous spaces, which is often much easier to work with than their Riemannian structure. The FIM is characterized by identifying the homogeneous space with a coset space, the group-theoretic CRB and its corollaries are presented, and its relationship to the Riemannian CRB is clarified. The application of our theory is illustrated using two examples from engineering: (i) estimation of the pose of a robot and (ii) sensor network localization. In particular, these examples demonstrate that homogeneous spaces provide a natural framework for studying statistical models that are invariant with respect to a group of symmetries.

RaggeDi: Diffusion-based State Estimation of Disordered Rags, Sheets, Towels and Blankets

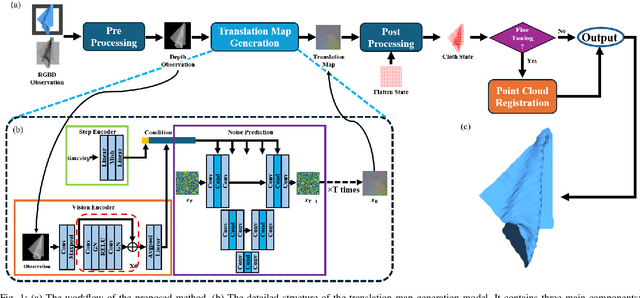
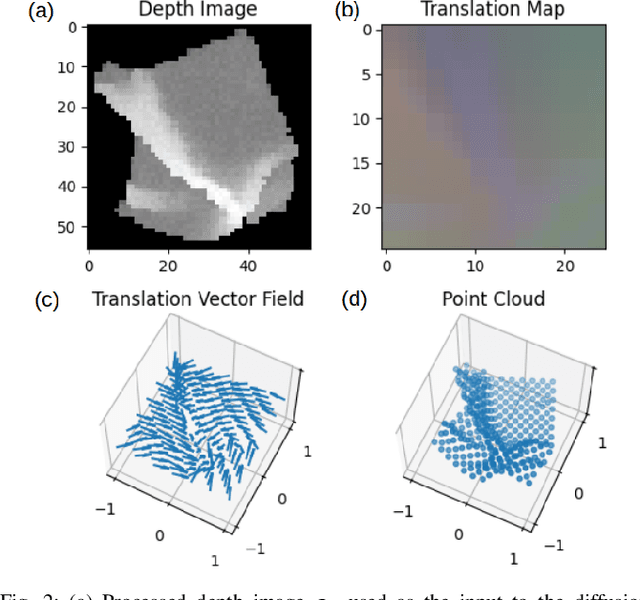
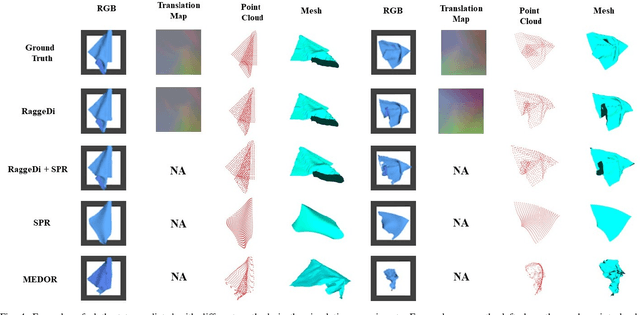
Cloth state estimation is an important problem in robotics. It is essential for the robot to know the accurate state to manipulate cloth and execute tasks such as robotic dressing, stitching, and covering/uncovering human beings. However, estimating cloth state accurately remains challenging due to its high flexibility and self-occlusion. This paper proposes a diffusion model-based pipeline that formulates the cloth state estimation as an image generation problem by representing the cloth state as an RGB image that describes the point-wise translation (translation map) between a pre-defined flattened mesh and the deformed mesh in a canonical space. Then we train a conditional diffusion-based image generation model to predict the translation map based on an observation. Experiments are conducted in both simulation and the real world to validate the performance of our method. Results indicate that our method outperforms two recent methods in both accuracy and speed.

Collaborative Fault-Identification & Reconstruction in Multi-Agent Systems

The conventional solutions for fault-detection, identification, and reconstruction (FDIR) require centralized decision-making mechanisms which are typically combinatorial in their nature, necessitating the design of an efficient distributed FDIR mechanism that is suitable for multi-agent applications. To this end, we develop a general framework for efficiently reconstructing a sparse vector being observed over a sensor network via nonlinear measurements. The proposed framework is used to design a distributed multi-agent FDIR algorithm based on a combination of the sequential convex programming (SCP) and the alternating direction method of multipliers (ADMM) optimization approaches. The proposed distributed FDIR algorithm can process a variety of inter-agent measurements (including distances, bearings, relative velocities, and subtended angles between agents) to identify the faulty agents and recover their true states. The effectiveness of the proposed distributed multi-agent FDIR approach is demonstrated by considering a numerical example in which the inter-agent distances are used to identify the faulty agents in a multi-agent configuration, as well as reconstruct their error vectors.

Distributed Gaussian Mixture PHD Filtering under Communication Constraints

The Gaussian Mixture Probability Hypothesis Density (GM-PHD) filter is an almost exact closed-form approximation to the Bayes-optimal multi-target tracking algorithm. Due to its optimality guarantees and ease of implementation, it has been studied extensively in the literature. However, the challenges involved in implementing the GM-PHD filter efficiently in a distributed (multi-sensor) setting have received little attention. The existing solutions for distributed PHD filtering either have a high computational and communication cost, making them infeasible for resource-constrained applications, or are unable to guarantee the asymptotic convergence of the distributed PHD algorithm to an optimal solution. In this paper, we develop a distributed GM-PHD filtering recursion that uses a probabilistic communication rule to limit the communication bandwidth of the algorithm, while ensuring asymptotic optimality of the algorithm. We derive the convergence properties of this recursion, which uses weighted average consensus of Gaussian mixtures (GMs) to lower (and asymptotically minimize) the Cauchy-Schwarz divergence between the sensors' local estimates. In addition, the proposed method is able to avoid the issue of false positives, which has previously been noted to impact the filtering performance of distributed multi-target tracking. Through numerical simulations, it is demonstrated that our proposed method is an effective solution for distributed multi-target tracking in resource-constrained sensor networks.

Recovery of Localization Errors in Sensor Networks using Inter-Agent Measurements

A practical challenge which arises in the operation of sensor networks is the presence of sensor faults, biases, or adversarial attacks, which can lead to significant errors incurring in the localization of the agents, thereby undermining the security and performance of the network. We consider the problem of identifying and correcting the localization errors using inter-agent measurements, such as the distances or bearings from one agent to another, which can serve as a redundant source of information about the sensor network's configuration. The problem is solved by searching for a block sparse solution to an underdetermined system of equations, where the sparsity is introduced via the fact that the number of localization errors is typically much lesser than the total number of agents. Unlike the existing works, our proposed method does not require the knowledge of the identities of the anchors, i.e., the agents that do not have localization errors. We characterize the necessary and sufficient conditions on the sensor network configuration under which a given number of localization errors can be uniquely identified and corrected using the proposed method. The applicability of our results is demonstrated numerically by processing inter-agent distance measurements using a sequential convex programming (SCP) algorithm to identify the localization errors in a sensor network.