Parameter Estimation on Homogeneous Spaces
Paper and Code
Oct 31, 2024


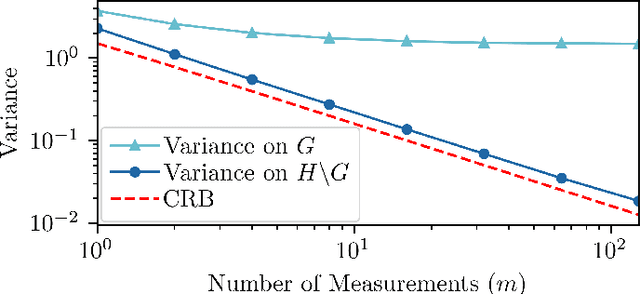
The Fisher Information Metric (FIM) and the associated Cram\'er-Rao Bound (CRB) are fundamental tools in statistical signal processing, which inform the efficient design of experiments and algorithms for estimating the underlying parameters. In this article, we investigate these concepts for the case where the parameters lie on a homogeneous space. Unlike the existing Fisher-Rao theory for general Riemannian manifolds, our focus is to leverage the group-theoretic structure of homogeneous spaces, which is often much easier to work with than their Riemannian structure. The FIM is characterized by identifying the homogeneous space with a coset space, the group-theoretic CRB and its corollaries are presented, and its relationship to the Riemannian CRB is clarified. The application of our theory is illustrated using two examples from engineering: (i) estimation of the pose of a robot and (ii) sensor network localization. In particular, these examples demonstrate that homogeneous spaces provide a natural framework for studying statistical models that are invariant with respect to a group of symmetries.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge