Variational Denoising for Variational Quantum Eigensolver

The variational quantum eigensolver (VQE) is a hybrid algorithm that has the potential to provide a quantum advantage in practical chemistry problems that are currently intractable on classical computers. VQE trains parameterized quantum circuits using a classical optimizer to approximate the eigenvalues and eigenstates of a given Hamiltonian. However, VQE faces challenges in task-specific design and machine-specific architecture, particularly when running on noisy quantum devices. This can have a negative impact on its trainability, accuracy, and efficiency, resulting in noisy quantum data. We propose variational denoising, an unsupervised learning method that employs a parameterized quantum neural network to improve the solution of VQE by learning from noisy VQE outputs. Our approach can significantly decrease energy estimation errors and increase fidelities with ground states compared to noisy input data for the H2 and LiH molecular Hamiltonians, and surprisingly only requires noisy data for training. Variational denoising can be integrated into quantum hardware, increasing its versatility as an end-to-end quantum processing for quantum data.

NeuRecover: Regression-Controlled Repair of Deep Neural Networks with Training History

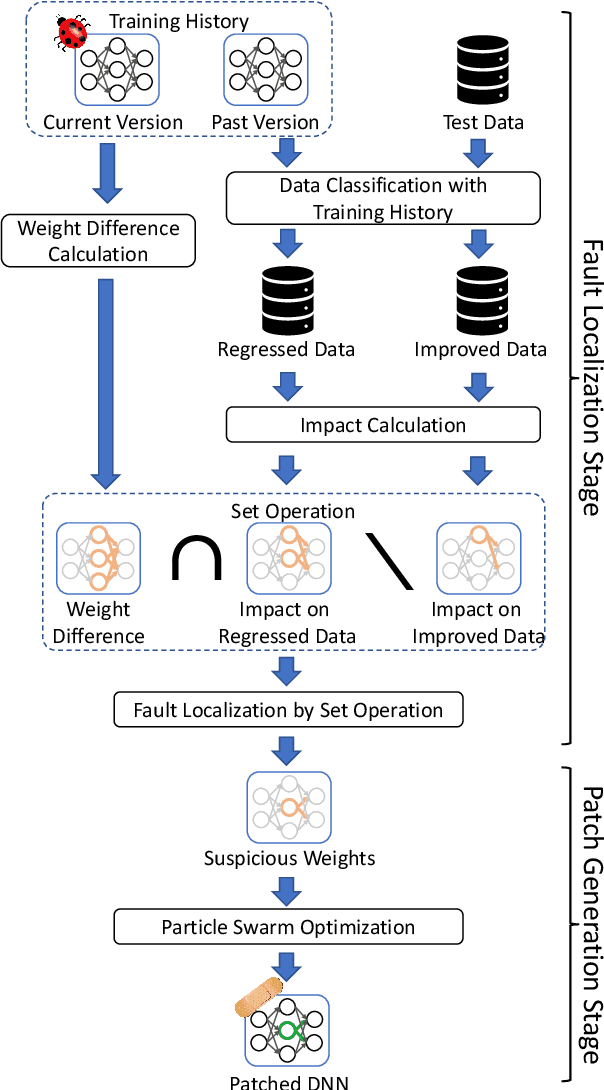
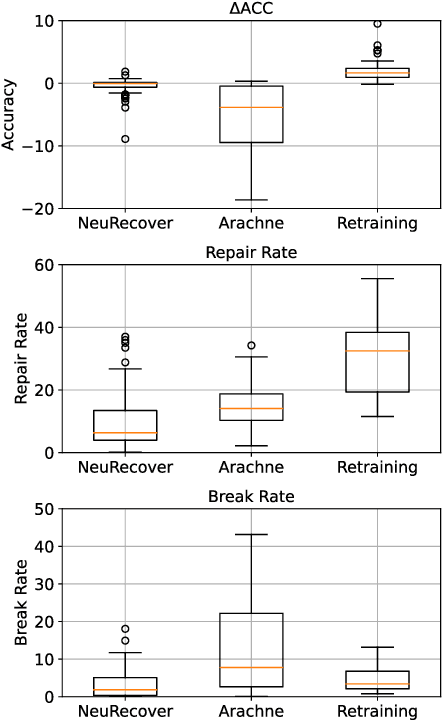
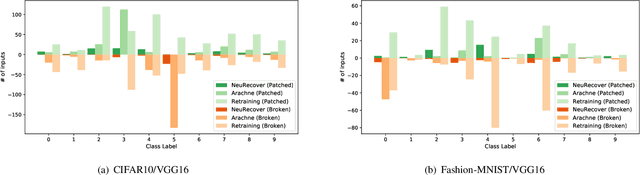
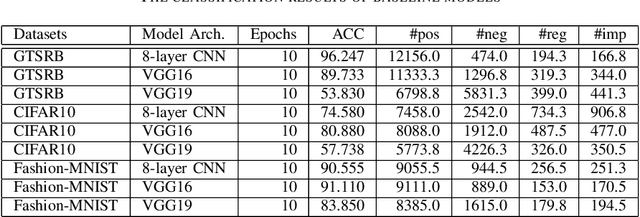
Systematic techniques to improve quality of deep neural networks (DNNs) are critical given the increasing demand for practical applications including safety-critical ones. The key challenge comes from the little controllability in updating DNNs. Retraining to fix some behavior often has a destructive impact on other behavior, causing regressions, i.e., the updated DNN fails with inputs correctly handled by the original one. This problem is crucial when engineers are required to investigate failures in intensive assurance activities for safety or trust. Search-based repair techniques for DNNs have potentials to tackle this challenge by enabling localized updates only on "responsible parameters" inside the DNN. However, the potentials have not been explored to realize sufficient controllability to suppress regressions in DNN repair tasks. In this paper, we propose a novel DNN repair method that makes use of the training history for judging which DNN parameters should be changed or not to suppress regressions. We implemented the method into a tool called NeuRecover and evaluated it with three datasets. Our method outperformed the existing method by achieving often less than a quarter, even a tenth in some cases, number of regressions. Our method is especially effective when the repair requirements are tight to fix specific failure types. In such cases, our method showed stably low rates (<2%) of regressions, which were in many cases a tenth of regressions caused by retraining.