Targeted Deep Learning: Framework, Methods, and Applications

Deep learning systems are typically designed to perform for a wide range of test inputs. For example, deep learning systems in autonomous cars are supposed to deal with traffic situations for which they were not specifically trained. In general, the ability to cope with a broad spectrum of unseen test inputs is called generalization. Generalization is definitely important in applications where the possible test inputs are known but plentiful or simply unknown, but there are also cases where the possible inputs are few and unlabeled but known beforehand. For example, medicine is currently interested in targeting treatments to individual patients; the number of patients at any given time is usually small (typically one), their diagnoses/responses/... are still unknown, but their general characteristics (such as genome information, protein levels in the blood, and so forth) are known before the treatment. We propose to call deep learning in such applications targeted deep learning. In this paper, we introduce a framework for targeted deep learning, and we devise and test an approach for adapting standard pipelines to the requirements of targeted deep learning. The approach is very general yet easy to use: it can be implemented as a simple data-preprocessing step. We demonstrate on a variety of real-world data that our approach can indeed render standard deep learning faster and more accurate when the test inputs are known beforehand.

DeepMoM: Robust Deep Learning With Median-of-Means

Data used in deep learning is notoriously problematic. For example, data are usually combined from diverse sources, rarely cleaned and vetted thoroughly, and sometimes corrupted on purpose. Intentional corruption that targets the weak spots of algorithms has been studied extensively under the label of "adversarial attacks." In contrast, the arguably much more common case of corruption that reflects the limited quality of data has been studied much less. Such "random" corruptions are due to measurement errors, unreliable sources, convenience sampling, and so forth. These kinds of corruption are common in deep learning, because data are rarely collected according to strict protocols -- in strong contrast to the formalized data collection in some parts of classical statistics. This paper concerns such corruption. We introduce an approach motivated by very recent insights into median-of-means and Le Cam's principle, we show that the approach can be readily implemented, and we demonstrate that it performs very well in practice. In conclusion, we believe that our approach is a very promising alternative to standard parameter training based on least-squares and cross-entropy loss.

Tuning-free ridge estimators for high-dimensional generalized linear models

Ridge estimators regularize the squared Euclidean lengths of parameters. Such estimators are mathematically and computationally attractive but involve tuning parameters that can be difficult to calibrate. In this paper, we show that ridge estimators can be modified such that tuning parameters can be avoided altogether. We also show that these modified versions can improve on the empirical prediction accuracies of standard ridge estimators combined with cross-validation, and we provide first theoretical guarantees.

Tuning parameter calibration for prediction in personalized medicine

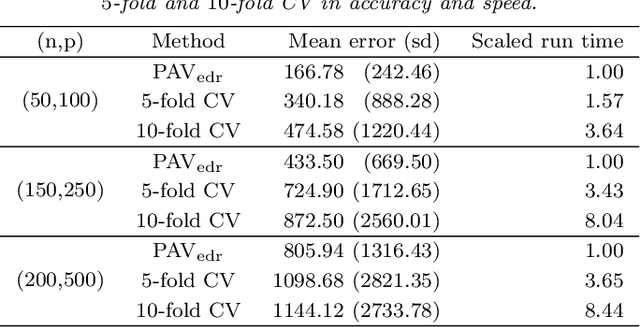
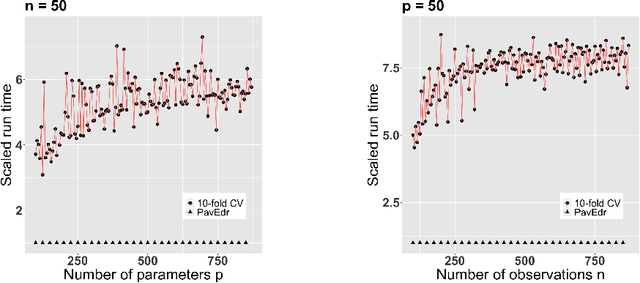
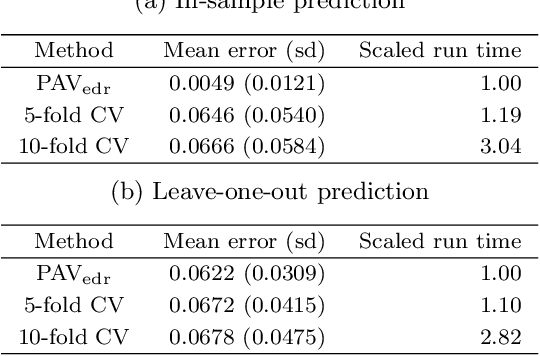
Personalized medicine has become an important part of medicine, for instance predicting individual drug responses based on genomic information. However, many current statistical methods are not tailored to this task, because they overlook the individual heterogeneity of patients. In this paper, we look at personalized medicine from a linear regression standpoint. We introduce an alternative version of the ridge estimator and target individuals by establishing a tuning parameter calibration scheme that minimizes prediction errors of individual patients. In stark contrast, classical schemes such as cross-validation minimize prediction errors only on average. We show that our pipeline is optimal in terms of oracle inequalities, fast, and highly effective both in simulations and on real data.