LLM-based Few-Shot Early Rumor Detection with Imitation Agent

Early Rumor Detection (EARD) aims to identify the earliest point at which a claim can be accurately classified based on a sequence of social media posts. This is especially challenging in data-scarce settings. While Large Language Models (LLMs) perform well in few-shot NLP tasks, they are not well-suited for time-series data and are computationally expensive for both training and inference. In this work, we propose a novel EARD framework that combines an autonomous agent and an LLM-based detection model, where the agent acts as a reliable decision-maker for \textit{early time point determination}, while the LLM serves as a powerful \textit{rumor detector}. This approach offers the first solution for few-shot EARD, necessitating only the training of a lightweight agent and allowing the LLM to remain training-free. Extensive experiments on four real-world datasets show our approach boosts performance across LLMs and surpasses existing EARD methods in accuracy and earliness.

Imitating Cost-Constrained Behaviors in Reinforcement Learning

Complex planning and scheduling problems have long been solved using various optimization or heuristic approaches. In recent years, imitation learning that aims to learn from expert demonstrations has been proposed as a viable alternative to solving these problems. Generally speaking, imitation learning is designed to learn either the reward (or preference) model or directly the behavioral policy by observing the behavior of an expert. Existing work in imitation learning and inverse reinforcement learning has focused on imitation primarily in unconstrained settings (e.g., no limit on fuel consumed by the vehicle). However, in many real-world domains, the behavior of an expert is governed not only by reward (or preference) but also by constraints. For instance, decisions on self-driving delivery vehicles are dependent not only on the route preferences/rewards (depending on past demand data) but also on the fuel in the vehicle and the time available. In such problems, imitation learning is challenging as decisions are not only dictated by the reward model but are also dependent on a cost-constrained model. In this paper, we provide multiple methods that match expert distributions in the presence of trajectory cost constraints through (a) Lagrangian-based method; (b) Meta-gradients to find a good trade-off between expected return and minimizing constraint violation; and (c) Cost-violation-based alternating gradient. We empirically show that leading imitation learning approaches imitate cost-constrained behaviors poorly and our meta-gradient-based approach achieves the best performance.

Preference-Aware Delivery Planning for Last-Mile Logistics

Optimizing delivery routes for last-mile logistics service is challenging and has attracted the attention of many researchers. These problems are usually modeled and solved as variants of vehicle routing problems (VRPs) with challenging real-world constraints (e.g., time windows, precedence). However, despite many decades of solid research on solving these VRP instances, we still see significant gaps between optimized routes and the routes that are actually preferred by the practitioners. Most of these gaps are due to the difference between what's being optimized, and what the practitioners actually care about, which is hard to be defined exactly in many instances. In this paper, we propose a novel hierarchical route optimizer with learnable parameters that combines the strength of both the optimization and machine learning approaches. Our hierarchical router first solves a zone-level Traveling Salesman Problem with learnable weights on various zone-level features; with the zone visit sequence fixed, we then solve the stop-level vehicle routing problem as a Shortest Hamiltonian Path problem. The Bayesian optimization approach is then introduced to allow us to adjust the weights to be assigned to different zone features used in solving the zone-level Traveling Salesman Problem. By using a real-world delivery dataset provided by the Amazon Last Mile Routing Research Challenge, we demonstrate the importance of having both the optimization and the machine learning components. We also demonstrate how we can use route-related features to identify instances that we might have difficulty with. This paves ways to further research on how we can tackle these difficult instances.

Multiscale Generative Models: Improving Performance of a Generative Model Using Feedback from Other Dependent Generative Models

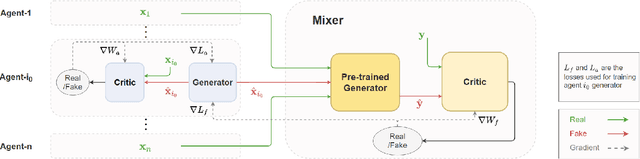
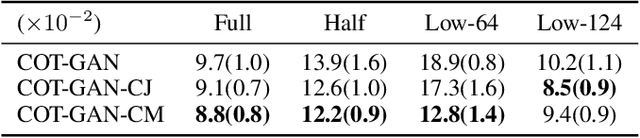
Realistic fine-grained multi-agent simulation of real-world complex systems is crucial for many downstream tasks such as reinforcement learning. Recent work has used generative models (GANs in particular) for providing high-fidelity simulation of real-world systems. However, such generative models are often monolithic and miss out on modeling the interaction in multi-agent systems. In this work, we take a first step towards building multiple interacting generative models (GANs) that reflects the interaction in real world. We build and analyze a hierarchical set-up where a higher-level GAN is conditioned on the output of multiple lower-level GANs. We present a technique of using feedback from the higher-level GAN to improve performance of lower-level GANs. We mathematically characterize the conditions under which our technique is impactful, including understanding the transfer learning nature of our set-up. We present three distinct experiments on synthetic data, time series data, and image domain, revealing the wide applicability of our technique.