Cell Biomechanical Modeling Based on Membrane Theory with Considering Speed Effect of Microinjection

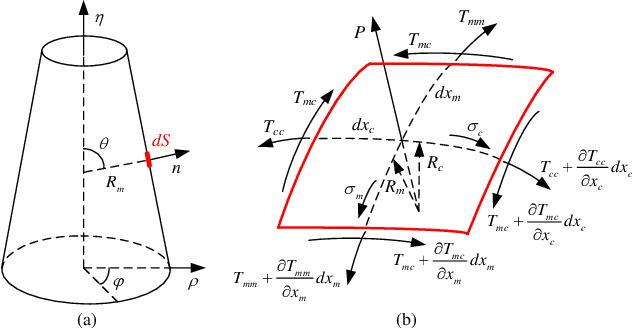
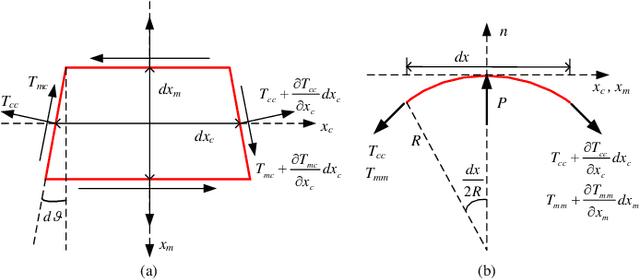
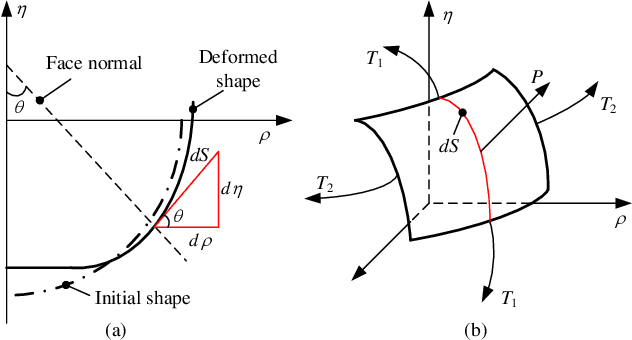
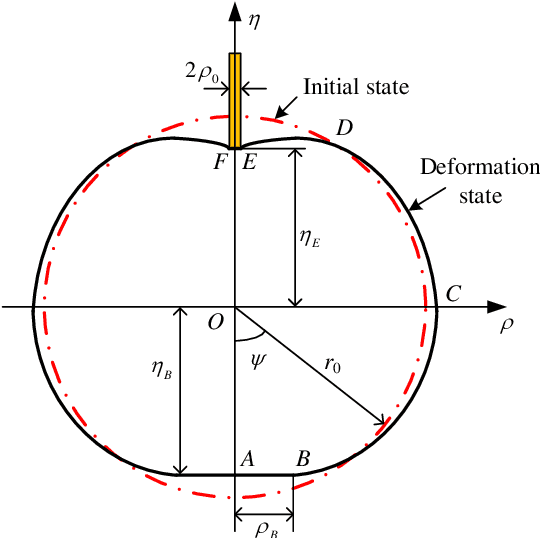
As an effective method to deliver external materials into biological cells, microinjection has been widely applied in the biomedical field. However, the cognition of cell mechanical property is still inadequate, which greatly limits the efficiency and success rate of injection. Thus, a new rate-dependent mechanical model based on membrane theory is proposed for the first time. In this model, an analytical equilibrium equation between the injection force and cell deformation is established by considering the speed effect of microinjection. Different from the traditional membrane-theory-based model, the elastic coefficient of the constitutive material in the proposed model is modified as a function of the injection velocity and acceleration, effectively simulating the influence of speeds on the mechanical responses and providing a more generalized and practical model. Using this model, other mechanical responses at different speeds can be also accurately predicted, including the distribution of membrane tension and stress and the deformed shape. To verify the validity of the model, numerical simulations and experiments are carried out. The results show that the proposed model can match the real mechanical responses well at different injection speeds.

A Fractional-Order Normalized Bouc-Wen Model for Piezoelectric Hysteresis Nonlinearity

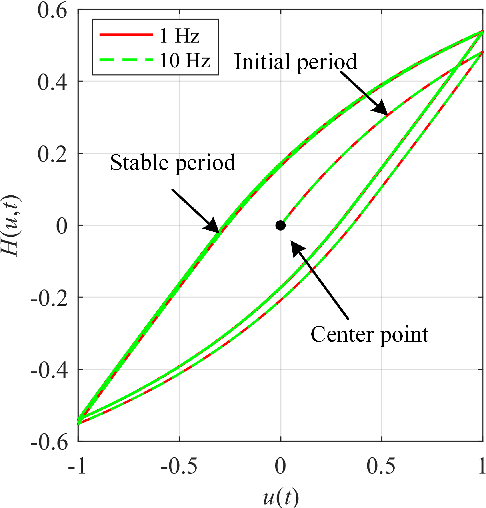
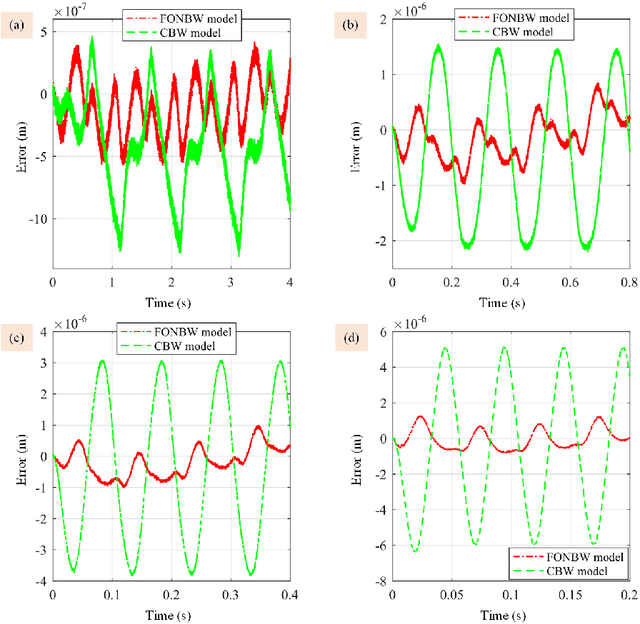
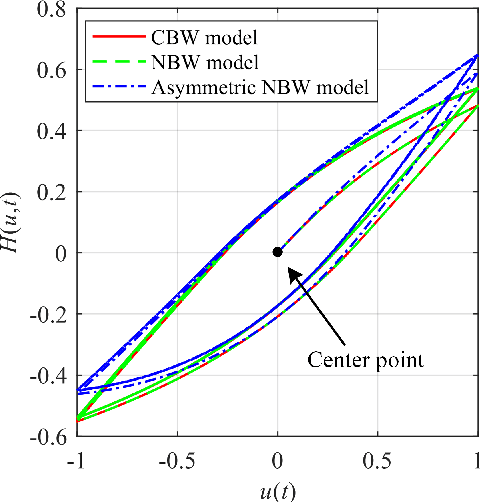
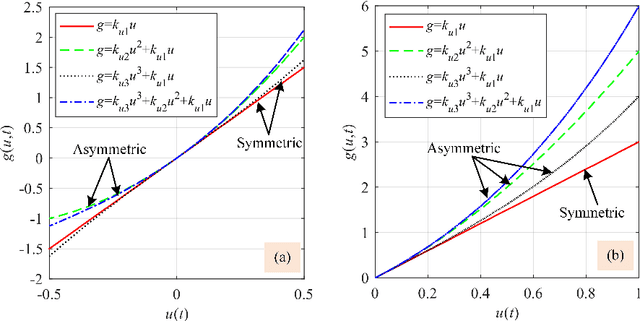
This paper presents a new fractional-order normalized Bouc-Wen (BW) (FONBW) model to describe the asymmetric and rate-dependent hysteresis nonlinearity of piezoelectric actuators (PEAs). In view of the fact that the classical BW (CBW) model is only efficient for the symmetric and rate-independent hysteresis description, the FONBW model is devoted to characterizing the asymmetric and rate-dependent behaviors of the hysteresis in PEAs by adopting a generalized input function and two fractional operators, respectively. Different from the traditional modified BW models, the proposed FONBW model also eliminates the redundancy of parameters in the CBW model via the normalization processing. By this way, the developed FONBW model has a relative simple mathematic expression with fewer parameters to simultaneously characterize the asymmetric and rate-dependent hysteresis behaviors of PEAs. Model parameters are identified by the self-adaptive differential evolution algorithm. To validate the effectiveness of the proposed model, a series of experimental studies are carried out on a PEA system. Results show that the proposed model is superior to the CBW model in accuracy.