Sheng-Yi Jiang
Sparsity Prior Regularized Q-learning for Sparse Action Tasks
May 19, 2021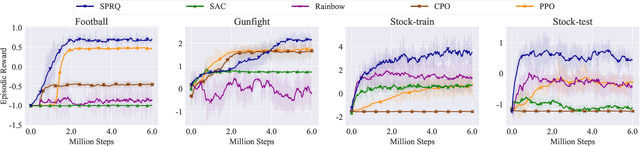

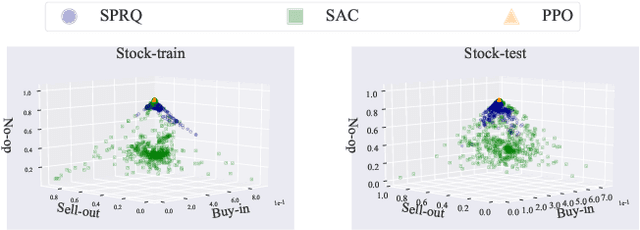
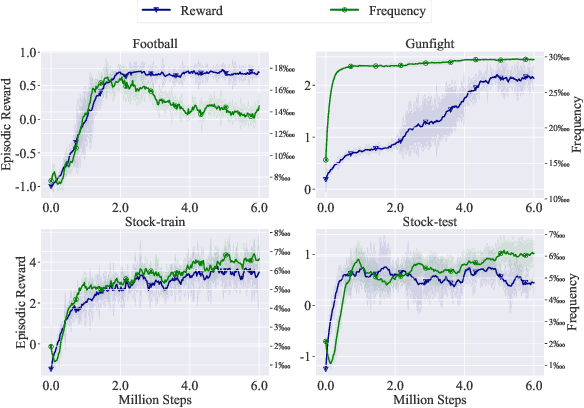
Abstract:In many decision-making tasks, some specific actions are limited in their frequency or total amounts, such as "fire" in the gunfight game and "buy/sell" in the stock trading. We name such actions as "sparse action". Sparse action often plays a crucial role in achieving good performance. However, their Q-values, estimated by \emph{classical Bellman update}, usually suffer from a large estimation error due to the sparsity of their samples. The \emph{greedy} policy could be greatly misled by the biased Q-function and takes sparse action aggressively, which leads to a huge sub-optimality. This paper constructs a reference distribution that assigns a low probability to sparse action and proposes a regularized objective with an explicit constraint to the reference distribution. Furthermore, we derive a regularized Bellman operator and a regularized optimal policy that can slow down the propagation of error and guide the agent to take sparse action more carefully. The experiment results demonstrate that our method achieves state-of-the-art performance on typical sparse action tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge