Optimal N-ary ECOC Matrices for Ensemble Classification

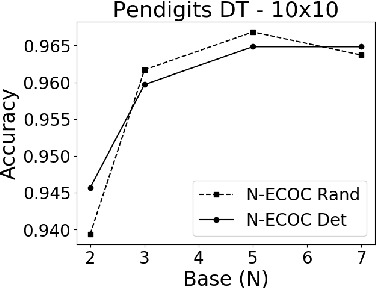
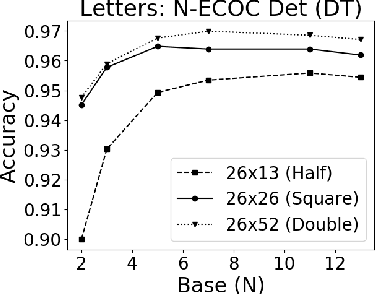
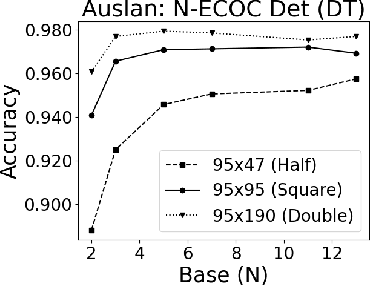
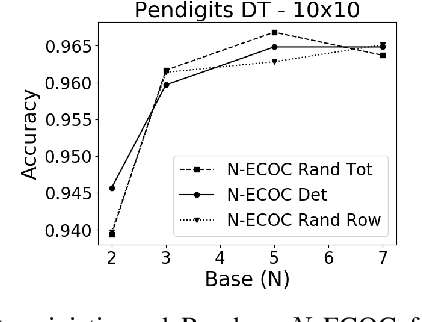
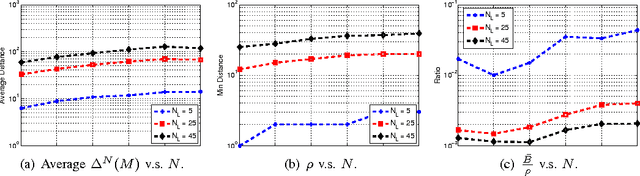
A new recursive construction of $N$-ary error-correcting output code (ECOC) matrices for ensemble classification methods is presented, generalizing the classic doubling construction for binary Hadamard matrices. Given any prime integer $N$, this deterministic construction generates base-$N$ symmetric square matrices $M$ of prime-power dimension having optimal minimum Hamming distance between any two of its rows and columns. Experimental results for six datasets demonstrate that using these deterministic coding matrices for $N$-ary ECOC classification yields comparable and in many cases higher accuracy compared to using randomly generated coding matrices. This is particular true when $N$ is adaptively chosen so that the dimension of $M$ matches closely with the number of classes in a dataset, which reduces the loss in minimum Hamming distance when $M$ is truncated to fit the dataset. This is verified through a distance formula for $M$ which shows that these adaptive matrices have significantly higher minimum Hamming distance in comparison to randomly generated ones.

Ensemble Learning using Error Correcting Output Codes: New Classification Error Bounds

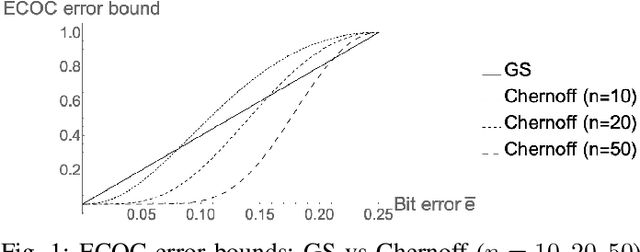
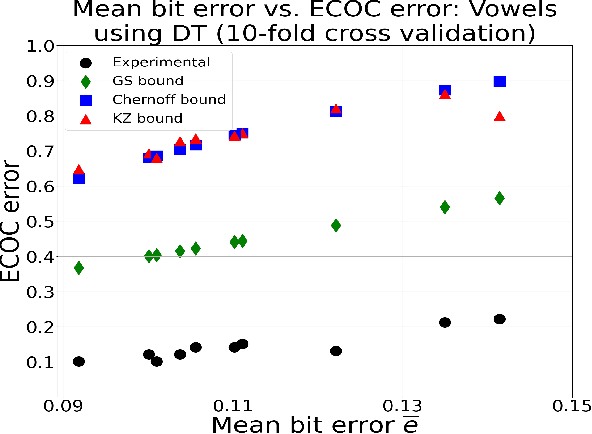
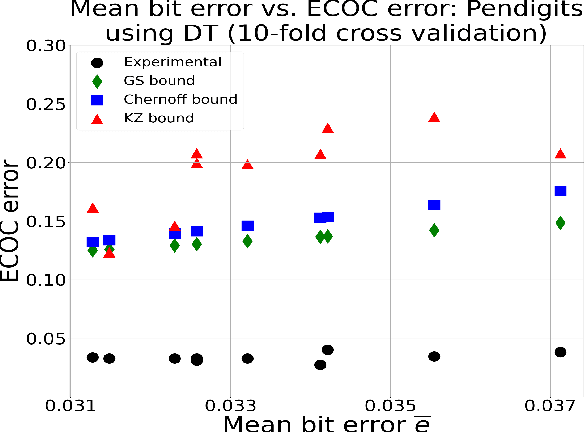
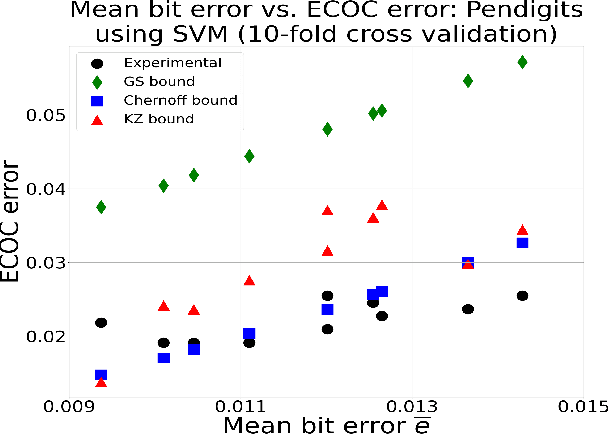
New bounds on classification error rates for the error-correcting output code (ECOC) approach in machine learning are presented. These bounds have exponential decay complexity with respect to codeword length and theoretically validate the effectiveness of the ECOC approach. Bounds are derived for two different models: the first under the assumption that all base classifiers are independent and the second under the assumption that all base classifiers are mutually correlated up to first-order. Moreover, we perform ECOC classification on six datasets and compare their error rates with our bounds to experimentally validate our work and show the effect of correlation on classification accuracy.

N-ary Error Correcting Coding Scheme

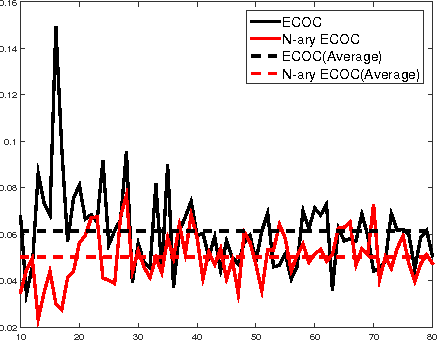
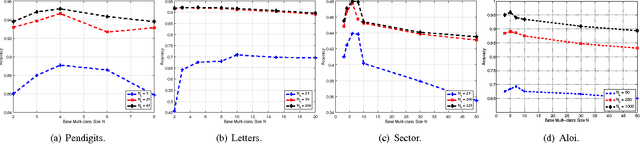
The coding matrix design plays a fundamental role in the prediction performance of the error correcting output codes (ECOC)-based multi-class task. {In many-class classification problems, e.g., fine-grained categorization, it is difficult to distinguish subtle between-class differences under existing coding schemes due to a limited choices of coding values.} In this paper, we investigate whether one can relax existing binary and ternary code design to $N$-ary code design to achieve better classification performance. {In particular, we present a novel $N$-ary coding scheme that decomposes the original multi-class problem into simpler multi-class subproblems, which is similar to applying a divide-and-conquer method.} The two main advantages of such a coding scheme are as follows: (i) the ability to construct more discriminative codes and (ii) the flexibility for the user to select the best $N$ for ECOC-based classification. We show empirically that the optimal $N$ (based on classification performance) lies in $[3, 10]$ with some trade-off in computational cost. Moreover, we provide theoretical insights on the dependency of the generalization error bound of an $N$-ary ECOC on the average base classifier generalization error and the minimum distance between any two codes constructed. Extensive experimental results on benchmark multi-class datasets show that the proposed coding scheme achieves superior prediction performance over the state-of-the-art coding methods.

On the Detection of Concept Changes in Time-Varying Data Stream by Testing Exchangeability

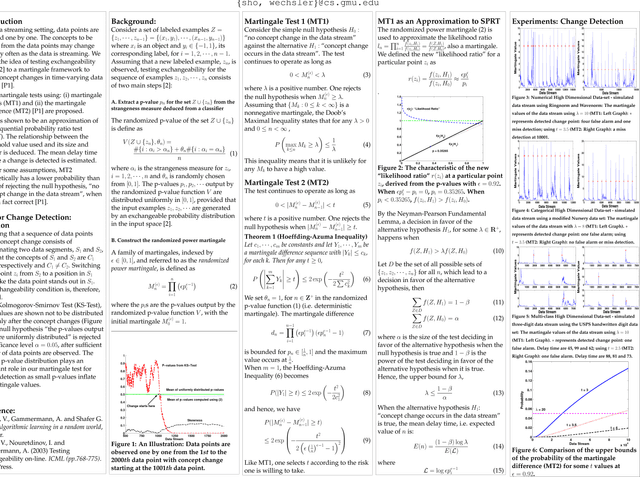
A martingale framework for concept change detection based on testing data exchangeability was recently proposed (Ho, 2005). In this paper, we describe the proposed change-detection test based on the Doob's Maximal Inequality and show that it is an approximation of the sequential probability ratio test (SPRT). The relationship between the threshold value used in the proposed test and its size and power is deduced from the approximation. The mean delay time before a change is detected is estimated using the average sample number of a SPRT. The performance of the test using various threshold values is examined on five different data stream scenarios simulated using two synthetic data sets. Finally, experimental results show that the test is effective in detecting changes in time-varying data streams simulated using three benchmark data sets.