N-ary Error Correcting Coding Scheme

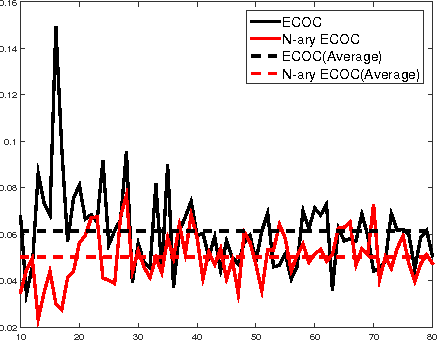
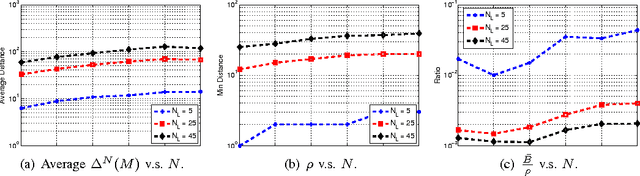
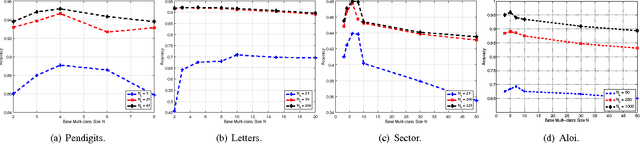
The coding matrix design plays a fundamental role in the prediction performance of the error correcting output codes (ECOC)-based multi-class task. {In many-class classification problems, e.g., fine-grained categorization, it is difficult to distinguish subtle between-class differences under existing coding schemes due to a limited choices of coding values.} In this paper, we investigate whether one can relax existing binary and ternary code design to $N$-ary code design to achieve better classification performance. {In particular, we present a novel $N$-ary coding scheme that decomposes the original multi-class problem into simpler multi-class subproblems, which is similar to applying a divide-and-conquer method.} The two main advantages of such a coding scheme are as follows: (i) the ability to construct more discriminative codes and (ii) the flexibility for the user to select the best $N$ for ECOC-based classification. We show empirically that the optimal $N$ (based on classification performance) lies in $[3, 10]$ with some trade-off in computational cost. Moreover, we provide theoretical insights on the dependency of the generalization error bound of an $N$-ary ECOC on the average base classifier generalization error and the minimum distance between any two codes constructed. Extensive experimental results on benchmark multi-class datasets show that the proposed coding scheme achieves superior prediction performance over the state-of-the-art coding methods.