Accurate Crop Yield Estimation of Blueberries using Deep Learning and Smart Drones

We present an AI pipeline that involves using smart drones equipped with computer vision to obtain a more accurate fruit count and yield estimation of the number of blueberries in a field. The core components are two object-detection models based on the YOLO deep learning architecture: a Bush Model that is able to detect blueberry bushes from images captured at low altitudes and at different angles, and a Berry Model that can detect individual berries that are visible on a bush. Together, both models allow for more accurate crop yield estimation by allowing intelligent control of the drone's position and camera to safely capture side-view images of bushes up close. In addition to providing experimental results for our models, which show good accuracy in terms of precision and recall when captured images are cropped around the foreground center bush, we also describe how to deploy our models to map out blueberry fields using different sampling strategies, and discuss the challenges of annotating very small objects (blueberries) and difficulties in evaluating the effectiveness of our models.

Optimal N-ary ECOC Matrices for Ensemble Classification

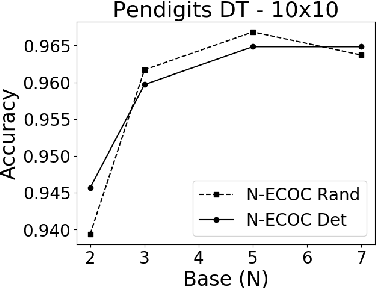
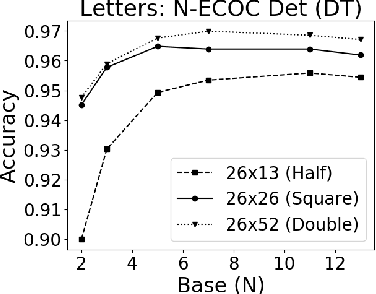
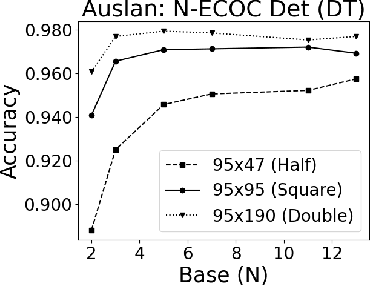
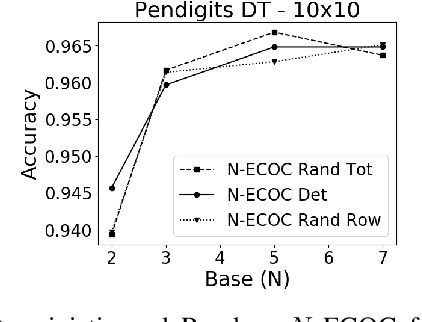
A new recursive construction of $N$-ary error-correcting output code (ECOC) matrices for ensemble classification methods is presented, generalizing the classic doubling construction for binary Hadamard matrices. Given any prime integer $N$, this deterministic construction generates base-$N$ symmetric square matrices $M$ of prime-power dimension having optimal minimum Hamming distance between any two of its rows and columns. Experimental results for six datasets demonstrate that using these deterministic coding matrices for $N$-ary ECOC classification yields comparable and in many cases higher accuracy compared to using randomly generated coding matrices. This is particular true when $N$ is adaptively chosen so that the dimension of $M$ matches closely with the number of classes in a dataset, which reduces the loss in minimum Hamming distance when $M$ is truncated to fit the dataset. This is verified through a distance formula for $M$ which shows that these adaptive matrices have significantly higher minimum Hamming distance in comparison to randomly generated ones.

Ensemble Learning using Error Correcting Output Codes: New Classification Error Bounds

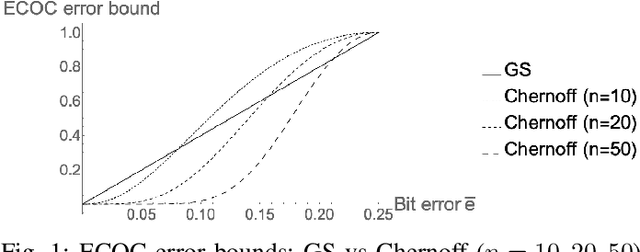
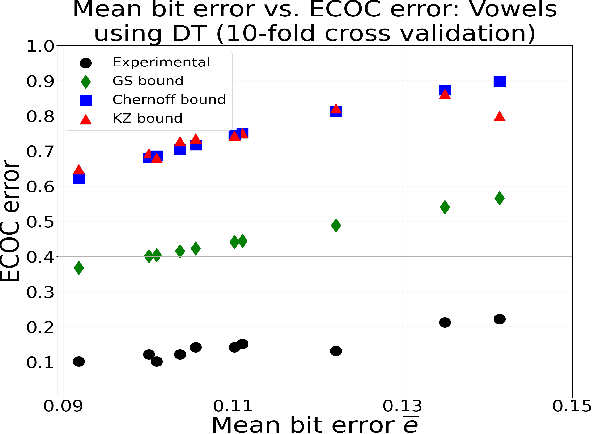
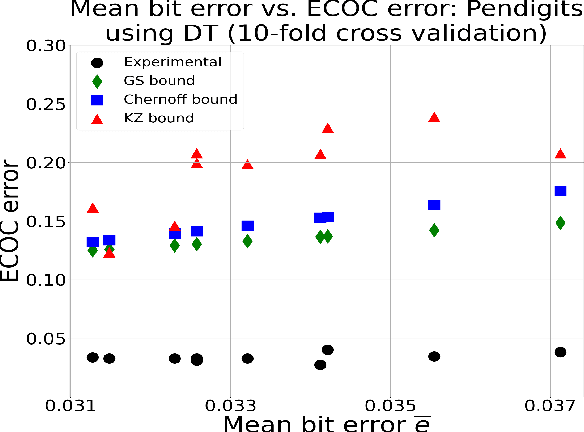
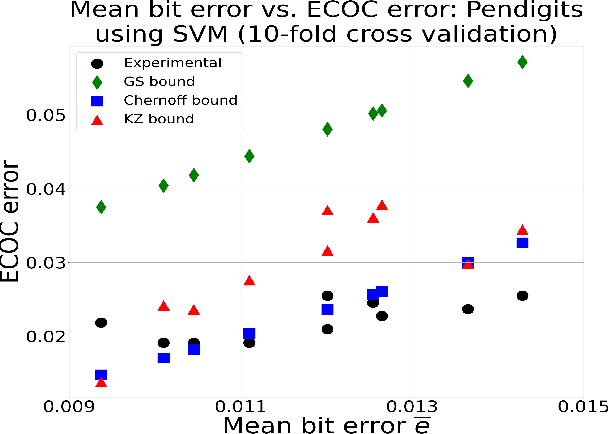
New bounds on classification error rates for the error-correcting output code (ECOC) approach in machine learning are presented. These bounds have exponential decay complexity with respect to codeword length and theoretically validate the effectiveness of the ECOC approach. Bounds are derived for two different models: the first under the assumption that all base classifiers are independent and the second under the assumption that all base classifiers are mutually correlated up to first-order. Moreover, we perform ECOC classification on six datasets and compare their error rates with our bounds to experimentally validate our work and show the effect of correlation on classification accuracy.