Chance Constrained Motion Planning for High-Dimensional Robots

This paper introduces Probabilistic Chekov (p-Chekov), a chance-constrained motion planning system that can be applied to high degree-of-freedom (DOF) robots under motion uncertainty and imperfect state information. Given process and observation noise models, it can find feasible trajectories which satisfy a user-specified bound over the probability of collision. Leveraging our previous work in deterministic motion planning which integrated trajectory optimization into a sparse roadmap framework, p-Chekov shows superiority in its planning speed for high-dimensional tasks. P-Chekov incorporates a linear-quadratic Gaussian motion planning approach into the estimation of the robot state probability distribution, applies quadrature theories to waypoint collision risk estimation, and adapts risk allocation approaches to assign allowable probabilities of failure among waypoints. Unlike other existing risk-aware planners, p-Chekov can be applied to high-DOF robotic planning tasks without the convexification of the environment. The experiment results in this paper show that this p-Chekov system can effectively reduce collision risk and satisfy user-specified chance constraints in typical real-world planning scenarios for high-DOF robots.

Improving Trajectory Optimization using a Roadmap Framework

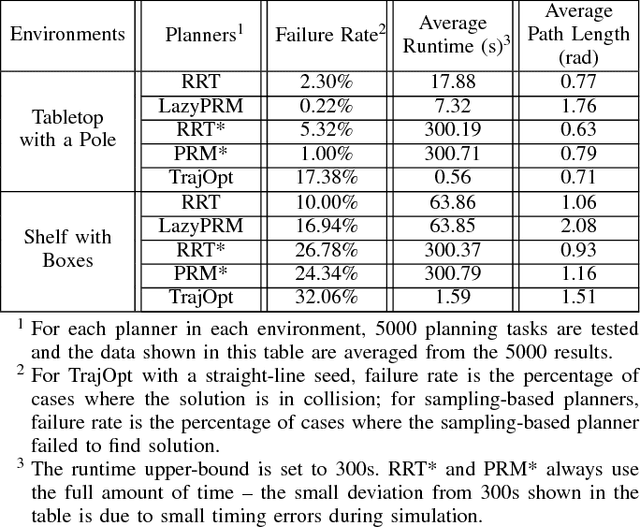
We present an evaluation of several representative sampling-based and optimization-based motion planners, and then introduce an integrated motion planning system which incorporates recent advances in trajectory optimization into a sparse roadmap framework. Through experiments in 4 common application scenarios with 5000 test cases each, we show that optimization-based or sampling-based planners alone are not effective for realistic problems where fast planning times are required. To the best of our knowledge, this is the first work that presents such a systematic and comprehensive evaluation of state-of-the-art motion planners, which are based on a significant amount of experiments. We then combine different stand-alone planners with trajectory optimization. The results show that the combination of our sparse roadmap and trajectory optimization provides superior performance over other standard sampling-based planners combinations. By using a multi-query roadmap instead of generating completely new trajectories for each planning problem, our approach allows for extensions such as persistent control policy information associated with a trajectory across planning problems. Also, the sub-optimality resulting from the sparsity of roadmap, as well as the unexpected disturbances from the environment, can both be overcome by the real-time trajectory optimization process.