Sergiy Pereverzyev Jr
Projection-Based 2.5D U-net Architecture for Fast Volumetric Segmentation
Feb 01, 2019
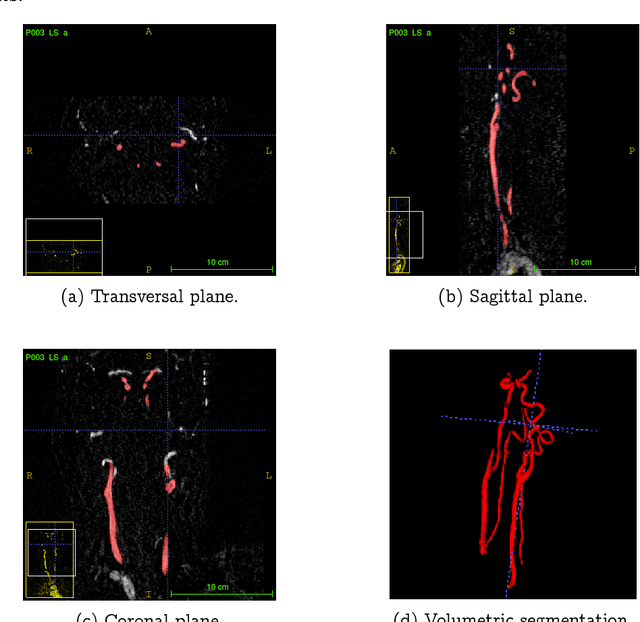

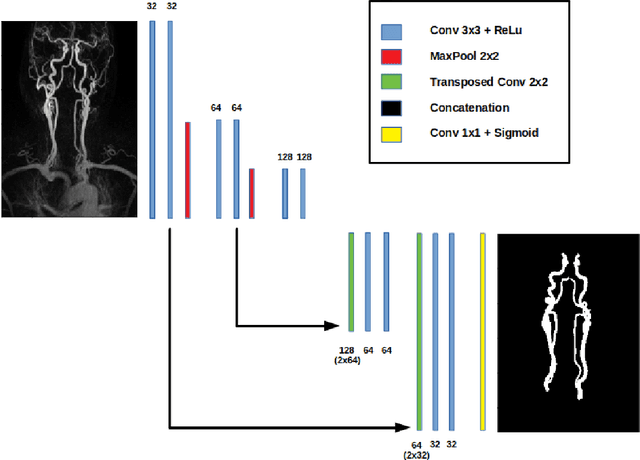
Abstract:Convolutional neural networks are state-of-the-art for various segmentation tasks. While for 2D images these networks are also computationally efficient, 3D convolutions have huge storage requirements and require long training time. To overcome this issue, we introduce a network structure for volumetric data without 3D convolution layers. The main idea is to integrate projection layers to transform the volumetric data to a sequence of images, where each image contains information of the full data. We then apply 2D convolutions to the projection images followed by lifting to a volumetric data. The proposed network structure can be trained in much less time than any 3D-network and still shows accurate performance for a sparse binary segmentation task.
Analysis of regularized Nyström subsampling for regression functions of low smoothness
Jun 03, 2018Abstract:This paper studies a Nystr\"om type subsampling approach to large kernel learning methods in the misspecified case, where the target function is not assumed to belong to the reproducing kernel Hilbert space generated by the underlying kernel. This case is less understood, in spite of its practical importance. To model such a case, the smoothness of target functions is described in terms of general source conditions. It is surprising that almost for the whole range of the source conditions, describing the misspecified case, the corresponding learning rate bounds can be achieved with just one value of the regularization parameter. This observation allows a formulation of mild conditions under which the plain Nystr\"om subsampling can be realized with subquadratic cost maintaining the guaranteed learning rates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge