Peter Mathé
Inverse learning in Hilbert scales
Feb 24, 2020

Abstract:We study the linear ill-posed inverse problem with noisy data in the statistical learning setting. Approximate reconstructions from random noisy data are sought with general regularization schemes in Hilbert scale. We discuss the rates of convergence for the regularized solution under the prior assumptions and a certain link condition. We express the error in terms of certain distance functions. For regression functions with smoothness given in terms of source conditions the error bound can then be explicitly established.
Convergence analysis of Tikhonov regularization for non-linear statistical inverse learning problems
Mar 01, 2019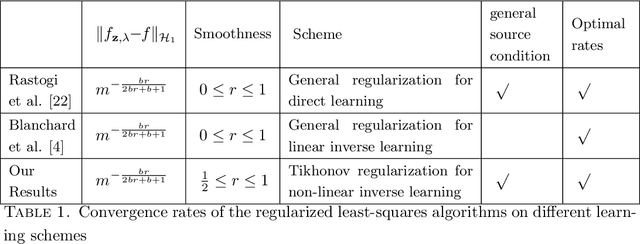
Abstract:We study a non-linear statistical inverse learning problem, where we observe the noisy image of a quantity through a non-linear operator at some random design points. We consider the widely used Tikhonov regularization (or method of regularization, MOR) approach to reconstruct the estimator of the quantity for the non-linear ill-posed inverse problem. The estimator is defined as the minimizer of a Tikhonov functional, which is the sum of a data misfit term and a quadratic penalty term. We develop a theoretical analysis for the minimizer of the Tikhonov regularization scheme using the ansatz of reproducing kernel Hilbert spaces. We discuss optimal rates of convergence for the proposed scheme, uniformly over classes of admissible solutions, defined through appropriate source conditions.
Analysis of regularized Nyström subsampling for regression functions of low smoothness
Jun 03, 2018Abstract:This paper studies a Nystr\"om type subsampling approach to large kernel learning methods in the misspecified case, where the target function is not assumed to belong to the reproducing kernel Hilbert space generated by the underlying kernel. This case is less understood, in spite of its practical importance. To model such a case, the smoothness of target functions is described in terms of general source conditions. It is surprising that almost for the whole range of the source conditions, describing the misspecified case, the corresponding learning rate bounds can be achieved with just one value of the regularization parameter. This observation allows a formulation of mild conditions under which the plain Nystr\"om subsampling can be realized with subquadratic cost maintaining the guaranteed learning rates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge