Statistical Inverse Problems in Hilbert Scales

In this paper, we study the Tikhonov regularization scheme in Hilbert scales for the nonlinear statistical inverse problem with a general noise. The regularizing norm in this scheme is stronger than the norm in Hilbert space. We focus on developing a theoretical analysis for this scheme based on the conditional stability estimates. We utilize the concept of the distance function to establish the high probability estimates of the direct and reconstruction error in Reproducing kernel Hilbert space setting. Further, the explicit rates of convergence in terms of sample size are established for the oversmoothing case and the regular case over the regularity class defined through appropriate source condition. Our results improve and generalize previous results obtained in related settings.

Inverse learning in Hilbert scales

We study the linear ill-posed inverse problem with noisy data in the statistical learning setting. Approximate reconstructions from random noisy data are sought with general regularization schemes in Hilbert scale. We discuss the rates of convergence for the regularized solution under the prior assumptions and a certain link condition. We express the error in terms of certain distance functions. For regression functions with smoothness given in terms of source conditions the error bound can then be explicitly established.

Convergence analysis of Tikhonov regularization for non-linear statistical inverse learning problems

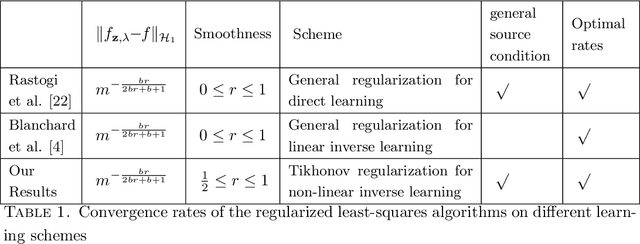
We study a non-linear statistical inverse learning problem, where we observe the noisy image of a quantity through a non-linear operator at some random design points. We consider the widely used Tikhonov regularization (or method of regularization, MOR) approach to reconstruct the estimator of the quantity for the non-linear ill-posed inverse problem. The estimator is defined as the minimizer of a Tikhonov functional, which is the sum of a data misfit term and a quadratic penalty term. We develop a theoretical analysis for the minimizer of the Tikhonov regularization scheme using the ansatz of reproducing kernel Hilbert spaces. We discuss optimal rates of convergence for the proposed scheme, uniformly over classes of admissible solutions, defined through appropriate source conditions.

Manifold regularization based on Nystr{ö}m type subsampling

In this paper, we study the Nystr{\"o}m type subsampling for large scale kernel methods to reduce the computational complexities of big data. We discuss the multi-penalty regularization scheme based on Nystr{\"o}m type subsampling which is motivated from well-studied manifold regularization schemes. We develop a theoretical analysis of multi-penalty least-square regularization scheme under the general source condition in vector-valued function setting, therefore the results can also be applied to multi-task learning problems. We achieve the optimal minimax convergence rates of multi-penalty regularization using the concept of effective dimension for the appropriate subsampling size. We discuss an aggregation approach based on linear function strategy to combine various Nystr{\"o}m approximants. Finally, we demonstrate the performance of multi-penalty regularization based on Nystr{\"o}m type subsampling on Caltech-101 data set for multi-class image classification and NSL-KDD benchmark data set for intrusion detection problem.

Optimal rates for the regularized learning algorithms under general source condition

We consider the learning algorithms under general source condition with the polynomial decay of the eigenvalues of the integral operator in vector-valued function setting. We discuss the upper convergence rates of Tikhonov regularizer under general source condition corresponding to increasing monotone index function. The convergence issues are studied for general regularization schemes by using the concept of operator monotone index functions in minimax setting. Further we also address the minimum possible error for any learning algorithm.