Shapley-Value-Based Graph Sparsification for GNN Inference

Graph sparsification is a key technique for improving inference efficiency in Graph Neural Networks by removing edges with minimal impact on predictions. GNN explainability methods generate local importance scores, which can be aggregated into global scores for graph sparsification. However, many explainability methods produce only non-negative scores, limiting their applicability for sparsification. In contrast, Shapley value based methods assign both positive and negative contributions to node predictions, offering a theoretically robust and fair allocation of importance by evaluating many subsets of graphs. Unlike gradient-based or perturbation-based explainers, Shapley values enable better pruning strategies that preserve influential edges while removing misleading or adversarial connections. Our approach shows that Shapley value-based graph sparsification maintains predictive performance while significantly reducing graph complexity, enhancing both interpretability and efficiency in GNN inference.

GNNShap: Fast and Accurate GNN Explanations using Shapley Values

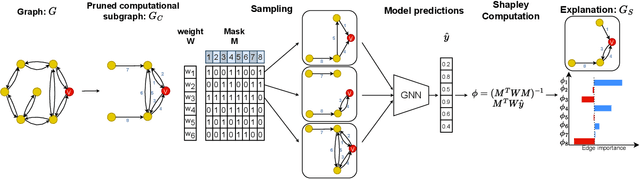
Graph neural networks (GNNs) are popular machine learning models for graphs with many applications across scientific domains. However, GNNs are considered black box models, and it is challenging to understand how the model makes predictions. Game theory-based Shapley value approaches are popular explanation methods in other domains but are not well-studied for graphs. Some studies have proposed Shapley value-based GNN explanations, yet they have several limitations: they consider limited samples to approximate Shapley values; some mainly focus on small and large coalition sizes, and they are an order of magnitude slower than other explanation methods, making them inapplicable to even moderate-size graphs. In this work, we propose GNNShap, which provides explanations for edges since they provide more natural explanations for graphs and more fine-grained explanations. We overcome the limitations by sampling from all coalition sizes, parallelizing the sampling on GPUs, and speeding up model predictions by batching. GNNShap gives better fidelity scores and faster explanations than baselines on real-world datasets.

Rank Position Forecasting in Car Racing

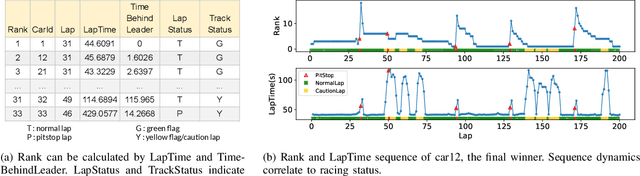
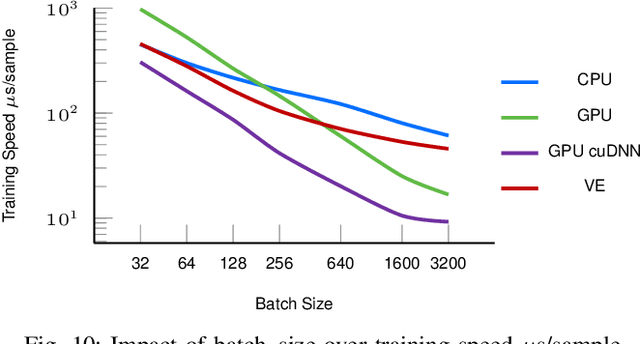
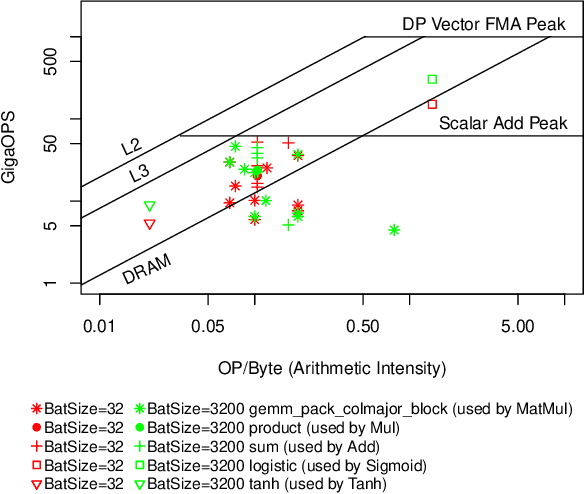
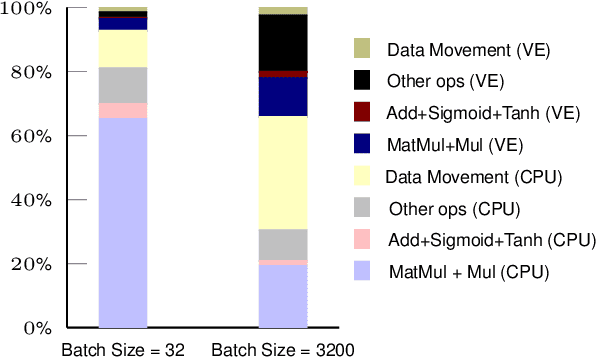
Forecasting is challenging since uncertainty resulted from exogenous factors exists. This work investigates the rank position forecasting problem in car racing, which predicts the rank positions at the future laps for cars. Among the many factors that bring changes to the rank positions, pit stops are critical but irregular and rare. We found existing methods, including statistical models, machine learning regression models, and state-of-the-art deep forecasting model based on encoder-decoder architecture, all have limitations in the forecasting. By elaborative analysis of pit stops events, we propose a deep model, RankNet, with the cause effects decomposition that modeling the rank position sequence and pit stop events separately. It also incorporates probabilistic forecasting to model the uncertainty inside each sub-model. Through extensive experiments, RankNet demonstrates a strong performance improvement over the baselines, e.g., MAE improves more than 10% consistently, and is also more stable when adapting to unseen new data. Details of model optimization, performance profiling are presented. It is promising to provide useful forecasting tools for the car racing analysis and shine a light on solutions to similar challenging issues in general forecasting problems.