Assessing high-order effects in feature importance via predictability decomposition

Leveraging the large body of work devoted in recent years to describe redundancy and synergy in multivariate interactions among random variables, we propose a novel approach to quantify cooperative effects in feature importance, one of the most used techniques for explainable artificial intelligence. In particular, we propose an adaptive version of a well-known metric of feature importance, named Leave One Covariate Out (LOCO), to disentangle high-order effects involving a given input feature in regression problems. LOCO is the reduction of the prediction error when the feature under consideration is added to the set of all the features used for regression. Instead of calculating the LOCO using all the features at hand, as in its standard version, our method searches for the multiplet of features that maximize LOCO and for the one that minimize it. This provides a decomposition of the LOCO as the sum of a two-body component and higher-order components (redundant and synergistic), also highlighting the features that contribute to building these high-order effects alongside the driving feature. We report the application to proton/pion discrimination from simulated detector measures by GEANT.

Information-Theoretic Progress Measures reveal Grokking is an Emergent Phase Transition

This paper studies emergent phenomena in neural networks by focusing on grokking where models suddenly generalize after delayed memorization. To understand this phase transition, we utilize higher-order mutual information to analyze the collective behavior (synergy) and shared properties (redundancy) between neurons during training. We identify distinct phases before grokking allowing us to anticipate when it occurs. We attribute grokking to an emergent phase transition caused by the synergistic interactions between neurons as a whole. We show that weight decay and weight initialization can enhance the emergent phase.

Higher-order mutual information reveals synergistic sub-networks for multi-neuron importance

Quantifying which neurons are important with respect to the classification decision of a trained neural network is essential for understanding their inner workings. Previous work primarily attributed importance to individual neurons. In this work, we study which groups of neurons contain synergistic or redundant information using a multivariate mutual information method called the O-information. We observe the first layer is dominated by redundancy suggesting general shared features (i.e. detecting edges) while the last layer is dominated by synergy indicating local class-specific features (i.e. concepts). Finally, we show the O-information can be used for multi-neuron importance. This can be demonstrated by re-training a synergistic sub-network, which results in a minimal change in performance. These results suggest our method can be used for pruning and unsupervised representation learning.

Local Granger Causality

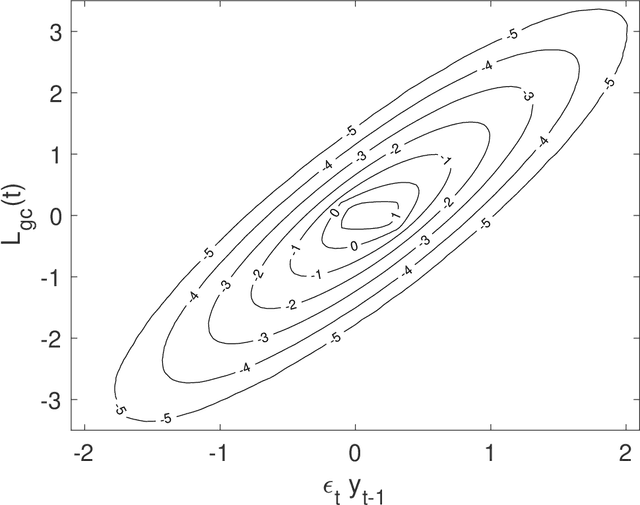
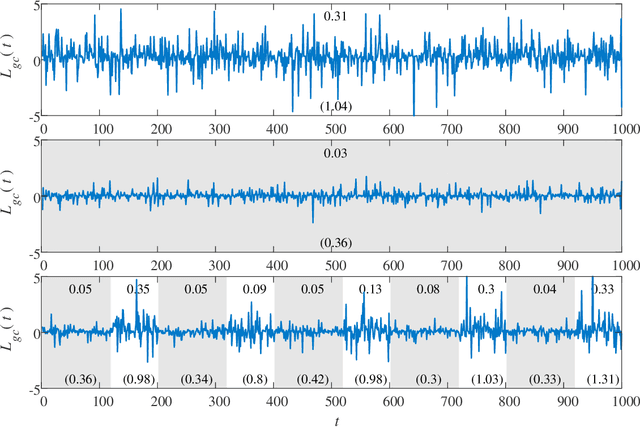
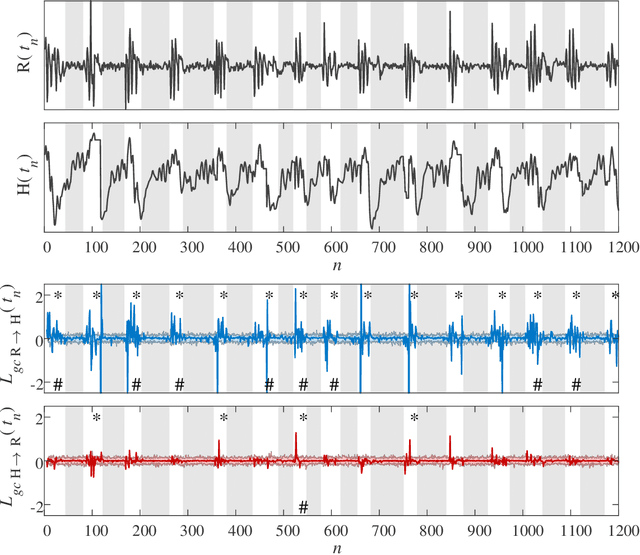
Granger causality is a statistical notion of causal influence based on prediction via vector autoregression. For Gaussian variables it is equivalent to transfer entropy, an information-theoretic measure of time-directed information transfer between jointly dependent processes. We exploit such equivalence and calculate exactly the 'local Granger causality', i.e. the profile of the information transfer at each discrete time point in Gaussian processes; in this frame Granger causality is the average of its local version. Our approach offers a robust and computationally fast method to follow the information transfer along the time history of linear stochastic processes, as well as of nonlinear complex systems studied in the Gaussian approximation.

Nonlinear parametric model for Granger causality of time series

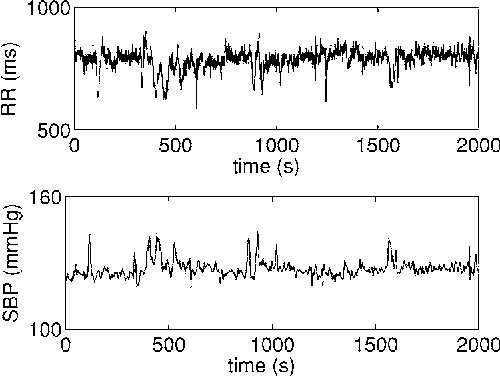
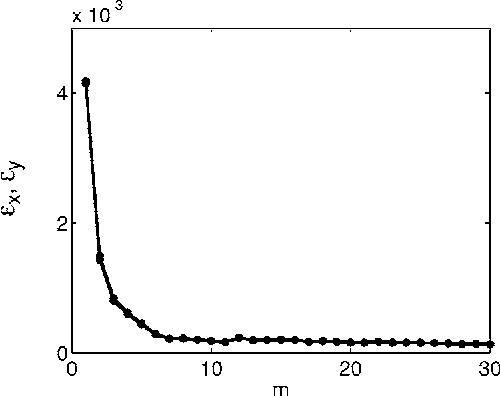
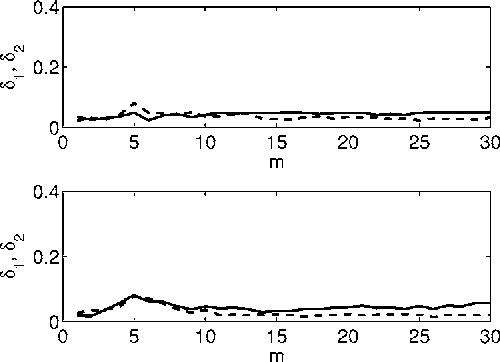
We generalize a previously proposed approach for nonlinear Granger causality of time series, based on radial basis function. The proposed model is not constrained to be additive in variables from the two time series and can approximate any function of these variables, still being suitable to evaluate causality. Usefulness of this measure of causality is shown in a physiological example and in the study of the feed-back loop in a model of excitatory and inhibitory neurons.