Yuri Antonacci
A method to assess Granger causality, isolation and autonomy in the time and frequency domains: theory and application to cerebrovascular variability
Jul 18, 2023Abstract:Concepts of Granger causality (GC) and Granger autonomy (GA) are central to assess the dynamics of coupled physiologic processes. While causality measures have been already proposed and applied in time and frequency domains, measures quantifying self-dependencies are still limited to the time-domain formulation and lack of a clear spectral representation. We embed into the classical linear parametric framework for computing GC from a driver random process X to a target process Y a measure of Granger Isolation (GI) quantifying the part of the dynamics of Y not originating from X, and a new spectral measure of GA assessing frequency-specific patterns of self-dependencies in Y. The measures are illustrated in theoretical simulations and applied to time series of mean arterial pressure and cerebral blood flow velocity obtained in subjects prone to develop postural syncope and healthy controls. Simulations show that GI is complementary to GC but not trivially related to it, while GA reflects the regularity of the internal dynamics of the analyzed target process. In the application to cerebrovascular interactions, spectral GA quantified the physiological response to postural stress of slow cerebral blood flow oscillations, while spectral GC and GI detected an altered response to postural stress in subjects prone to syncope, likely related to impaired cerebral autoregulation. The new spectral measures of GI and GA are useful complements to GC for the analysis of interacting oscillatory processes, and detect physiological and pathological responses to postural stress which cannot be traced in the time domain. The assessment of causality, isolation and autonomy opens new perspectives for the analysis of coupled biological processes in both physiological and clinical investigations.
Local Granger Causality
Oct 26, 2020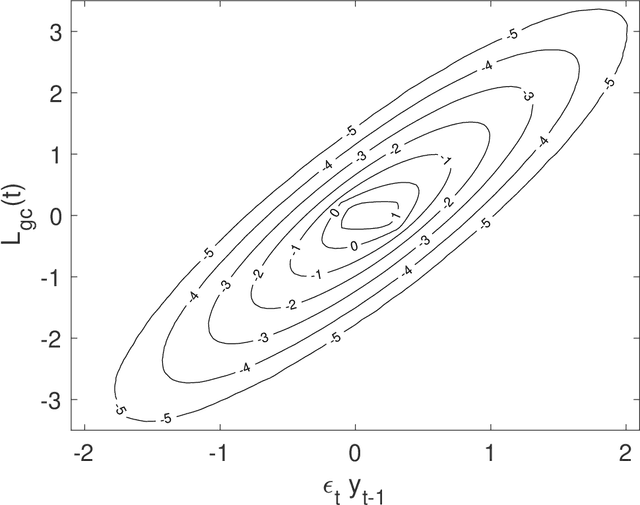
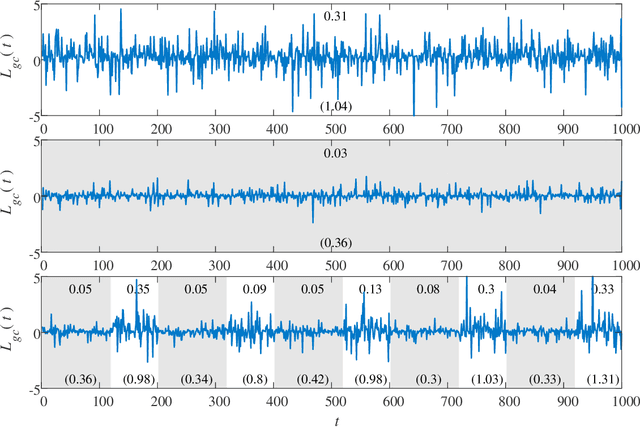
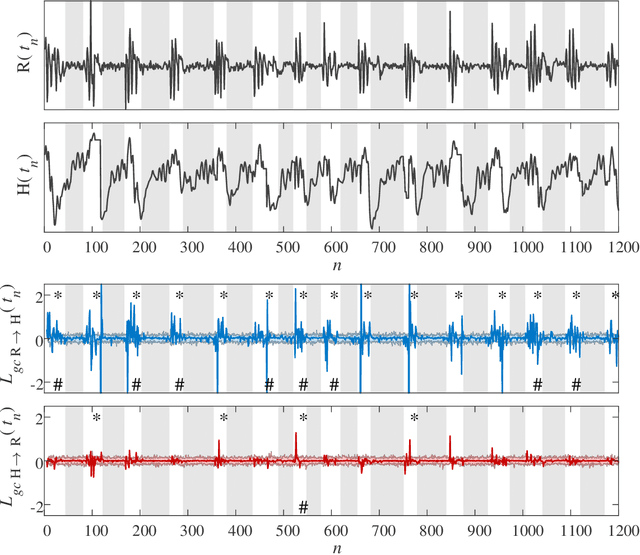

Abstract:Granger causality is a statistical notion of causal influence based on prediction via vector autoregression. For Gaussian variables it is equivalent to transfer entropy, an information-theoretic measure of time-directed information transfer between jointly dependent processes. We exploit such equivalence and calculate exactly the 'local Granger causality', i.e. the profile of the information transfer at each discrete time point in Gaussian processes; in this frame Granger causality is the average of its local version. Our approach offers a robust and computationally fast method to follow the information transfer along the time history of linear stochastic processes, as well as of nonlinear complex systems studied in the Gaussian approximation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge