NECO: NEural Collapse Based Out-of-distribution detection

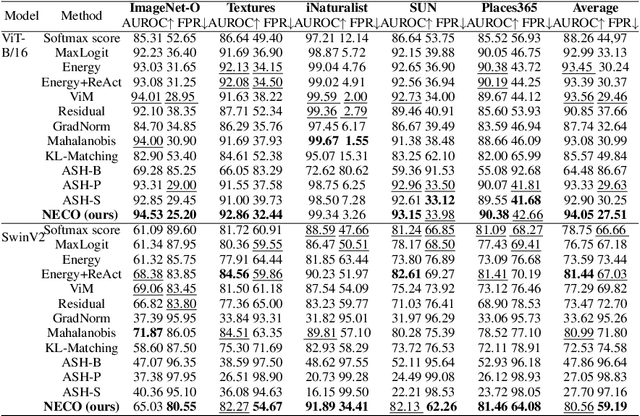
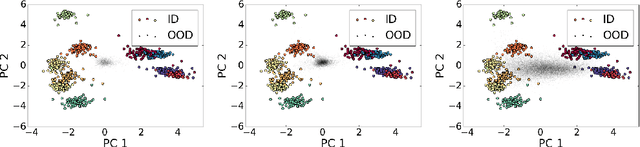
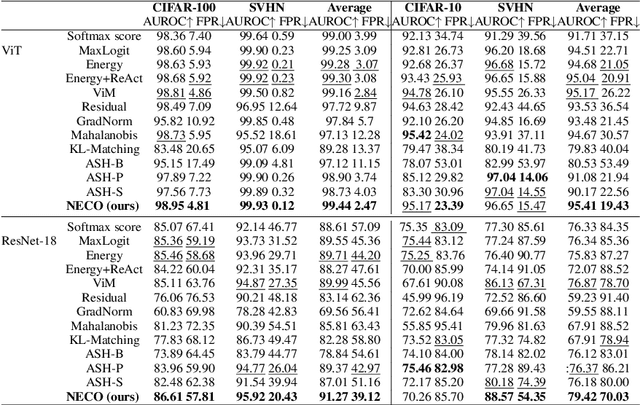
Detecting out-of-distribution (OOD) data is a critical challenge in machine learning due to model overconfidence, often without awareness of their epistemological limits. We hypothesize that ``neural collapse'', a phenomenon affecting in-distribution data for models trained beyond loss convergence, also influences OOD data. To benefit from this interplay, we introduce NECO, a novel post-hoc method for OOD detection, which leverages the geometric properties of ``neural collapse'' and of principal component spaces to identify OOD data. Our extensive experiments demonstrate that NECO achieves state-of-the-art results on both small and large-scale OOD detection tasks while exhibiting strong generalization capabilities across different network architectures. Furthermore, we provide a theoretical explanation for the effectiveness of our method in OOD detection. We plan to release the code after the anonymity period.

Hierarchical Gaussian Processes with Wasserstein-2 Kernels

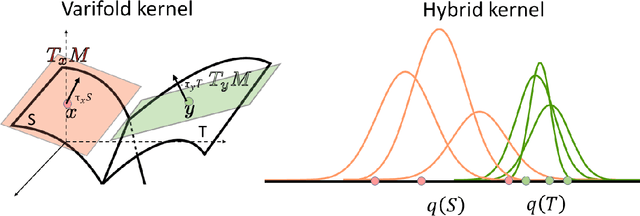
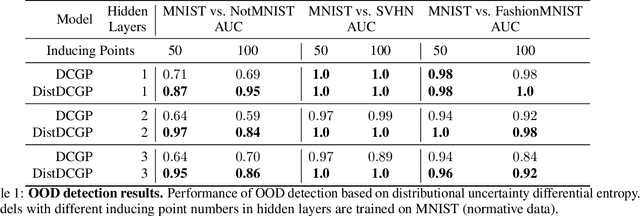
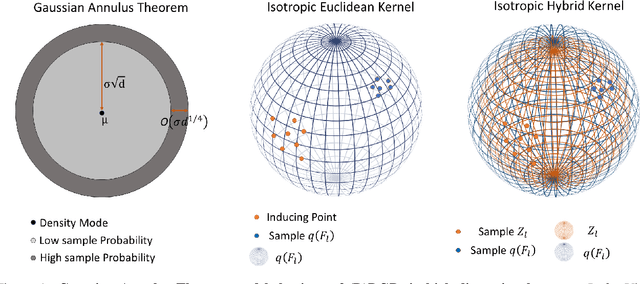
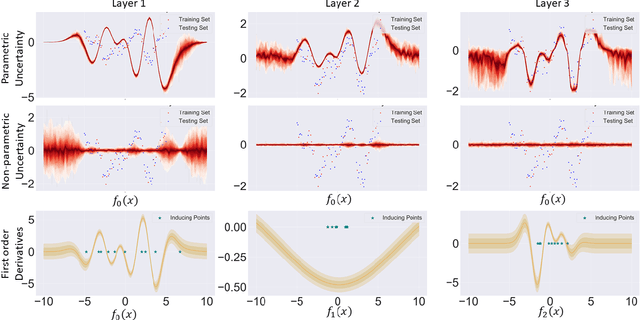
We investigate the usefulness of Wasserstein-2 kernels in the context of hierarchical Gaussian Processes. Stemming from an observation that stacking Gaussian Processes severely diminishes the model's ability to detect outliers, which when combined with non-zero mean functions, further extrapolates low variance to regions with low training data density, we posit that directly taking into account the variance in the computation of Wasserstein-2 kernels is of key importance towards maintaining outlier status as we progress through the hierarchy. We propose two new models operating in Wasserstein space which can be seen as equivalents to Deep Kernel Learning and Deep GPs. Through extensive experiments, we show improved performance on large scale datasets and improved out-of-distribution detection on both toy and real data.