Hierarchical Gaussian Processes with Wasserstein-2 Kernels

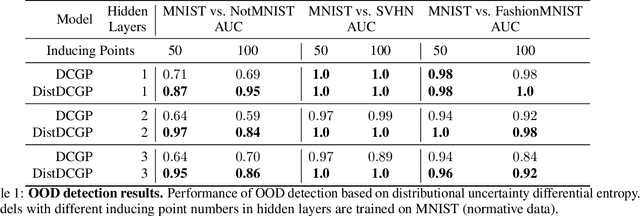
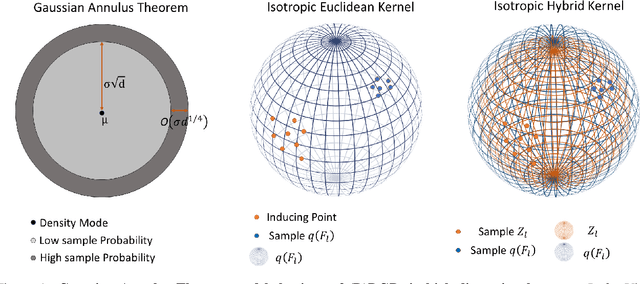
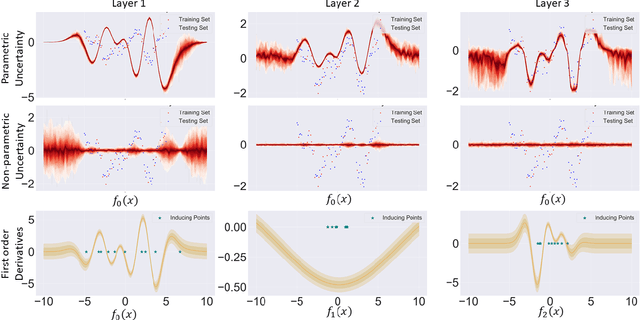
We investigate the usefulness of Wasserstein-2 kernels in the context of hierarchical Gaussian Processes. Stemming from an observation that stacking Gaussian Processes severely diminishes the model's ability to detect outliers, which when combined with non-zero mean functions, further extrapolates low variance to regions with low training data density, we posit that directly taking into account the variance in the computation of Wasserstein-2 kernels is of key importance towards maintaining outlier status as we progress through the hierarchy. We propose two new models operating in Wasserstein space which can be seen as equivalents to Deep Kernel Learning and Deep GPs. Through extensive experiments, we show improved performance on large scale datasets and improved out-of-distribution detection on both toy and real data.