Robust Reinforcement Learning with Dynamic Distortion Risk Measures

In a reinforcement learning (RL) setting, the agent's optimal strategy heavily depends on her risk preferences and the underlying model dynamics of the training environment. These two aspects influence the agent's ability to make well-informed and time-consistent decisions when facing testing environments. In this work, we devise a framework to solve robust risk-aware RL problems where we simultaneously account for environmental uncertainty and risk with a class of dynamic robust distortion risk measures. Robustness is introduced by considering all models within a Wasserstein ball around a reference model. We estimate such dynamic robust risk measures using neural networks by making use of strictly consistent scoring functions, derive policy gradient formulae using the quantile representation of distortion risk measures, and construct an actor-critic algorithm to solve this class of robust risk-aware RL problems. We demonstrate the performance of our algorithm on a portfolio allocation example.

Kullback-Leibler Barycentre of Stochastic Processes

We consider the problem where an agent aims to combine the views and insights of different experts' models. Specifically, each expert proposes a diffusion process over a finite time horizon. The agent then combines the experts' models by minimising the weighted Kullback-Leibler divergence to each of the experts' models. We show existence and uniqueness of the barycentre model and proof an explicit representation of the Radon-Nikodym derivative relative to the average drift model. We further allow the agent to include their own constraints, which results in an optimal model that can be seen as a distortion of the experts' barycentre model to incorporate the agent's constraints. Two deep learning algorithms are proposed to find the optimal drift of the combined model, allowing for efficient simulations. The first algorithm aims at learning the optimal drift by matching the change of measure, whereas the second algorithm leverages the notion of elicitability to directly estimate the value function. The paper concludes with a extended application to combine implied volatility smiles models that were estimated on different datasets.

Learning conditional distributions on continuous spaces

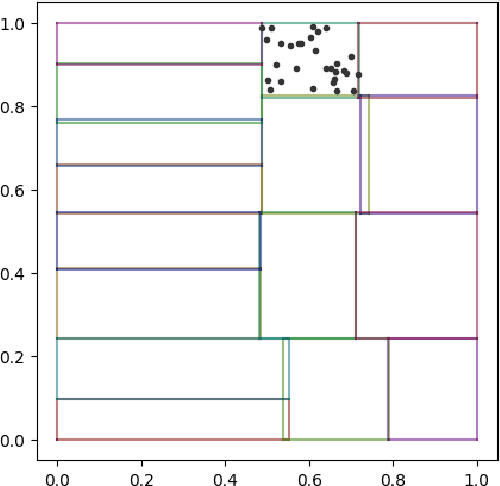
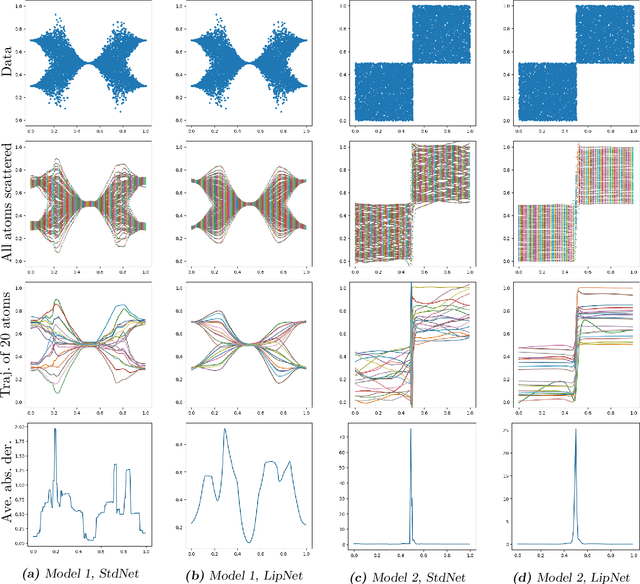
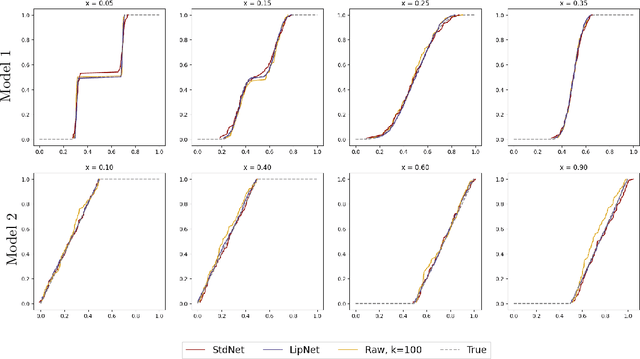
We investigate sample-based learning of conditional distributions on multi-dimensional unit boxes, allowing for different dimensions of the feature and target spaces. Our approach involves clustering data near varying query points in the feature space to create empirical measures in the target space. We employ two distinct clustering schemes: one based on a fixed-radius ball and the other on nearest neighbors. We establish upper bounds for the convergence rates of both methods and, from these bounds, deduce optimal configurations for the radius and the number of neighbors. We propose to incorporate the nearest neighbors method into neural network training, as our empirical analysis indicates it has better performance in practice. For efficiency, our training process utilizes approximate nearest neighbors search with random binary space partitioning. Additionally, we employ the Sinkhorn algorithm and a sparsity-enforced transport plan. Our empirical findings demonstrate that, with a suitably designed structure, the neural network has the ability to adapt to a suitable level of Lipschitz continuity locally. For reproducibility, our code is available at \url{https://github.com/zcheng-a/LCD_kNN}.

Eliciting Risk Aversion with Inverse Reinforcement Learning via Interactive Questioning

This paper proposes a novel framework for identifying an agent's risk aversion using interactive questioning. Our study is conducted in two scenarios: a one-period case and an infinite horizon case. In the one-period case, we assume that the agent's risk aversion is characterized by a cost function of the state and a distortion risk measure. In the infinite horizon case, we model risk aversion with an additional component, a discount factor. Assuming the access to a finite set of candidates containing the agent's true risk aversion, we show that asking the agent to demonstrate her optimal policies in various environment, which may depend on their previous answers, is an effective means of identifying the agent's risk aversion. Specifically, we prove that the agent's risk aversion can be identified as the number of questions tends to infinity, and the questions are randomly designed. We also develop an algorithm for designing optimal questions and provide empirical evidence that our method learns risk aversion significantly faster than randomly designed questions in simulations. Our framework has important applications in robo-advising and provides a new approach for identifying an agent's risk preferences.

Robust Risk-Aware Option Hedging

The objectives of option hedging/trading extend beyond mere protection against downside risks, with a desire to seek gains also driving agent's strategies. In this study, we showcase the potential of robust risk-aware reinforcement learning (RL) in mitigating the risks associated with path-dependent financial derivatives. We accomplish this by leveraging a policy gradient approach that optimises robust risk-aware performance criteria. We specifically apply this methodology to the hedging of barrier options, and highlight how the optimal hedging strategy undergoes distortions as the agent moves from being risk-averse to risk-seeking. As well as how the agent robustifies their strategy. We further investigate the performance of the hedge when the data generating process (DGP) varies from the training DGP, and demonstrate that the robust strategies outperform the non-robust ones.

FuNVol: A Multi-Asset Implied Volatility Market Simulator using Functional Principal Components and Neural SDEs

This paper introduces a new approach for generating sequences of implied volatility (IV) surfaces across multiple assets that is faithful to historical prices. We do so using a combination of functional data analysis and neural stochastic differential equations (SDEs) combined with a probability integral transform penalty to reduce model misspecification. We demonstrate that learning the joint dynamics of IV surfaces and prices produces market scenarios that are consistent with historical features and lie within the sub-manifold of surfaces that are free of static arbitrage.

Distributional Method for Risk Averse Reinforcement Learning

We introduce a distributional method for learning the optimal policy in risk averse Markov decision process with finite state action spaces, latent costs, and stationary dynamics. We assume sequential observations of states, actions, and costs and assess the performance of a policy using dynamic risk measures constructed from nested Kusuoka-type conditional risk mappings. For such performance criteria, randomized policies may outperform deterministic policies, therefore, the candidate policies lie in the d-dimensional simplex where d is the cardinality of the action space. Existing risk averse reinforcement learning methods seldom concern randomized policies, na\"ive extensions to current setting suffer from the curse of dimensionality. By exploiting certain structures embedded in the corresponding dynamic programming principle, we propose a distributional learning method for seeking the optimal policy. The conditional distribution of the value function is casted into a specific type of function, which is chosen with in mind the ease of risk averse optimization. We use a deep neural network to approximate said function, illustrate that the proposed method avoids the curse of dimensionality in the exploration phase, and explore the method's performance with a wide range of model parameters that are picked randomly.

Conditionally Elicitable Dynamic Risk Measures for Deep Reinforcement Learning

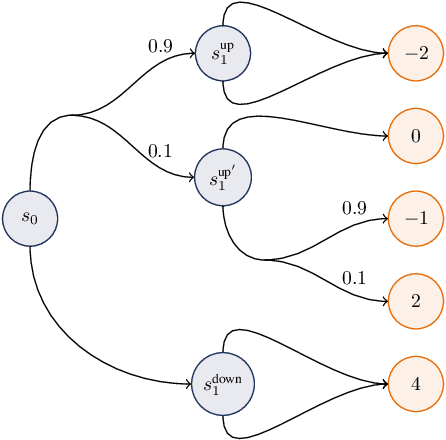
We propose a novel framework to solve risk-sensitive reinforcement learning (RL) problems where the agent optimises time-consistent dynamic spectral risk measures. Based on the notion of conditional elicitability, our methodology constructs (strictly consistent) scoring functions that are used as penalizers in the estimation procedure. Our contribution is threefold: we (i) devise an efficient approach to estimate a class of dynamic spectral risk measures with deep neural networks, (ii) prove that these dynamic spectral risk measures may be approximated to any arbitrary accuracy using deep neural networks, and (iii) develop a risk-sensitive actor-critic algorithm that uses full episodes and does not require any additional nested transitions. We compare our conceptually improved reinforcement learning algorithm with the nested simulation approach and illustrate its performance in two settings: statistical arbitrage and portfolio allocation on both simulated and real data.

Reinforcement Learning with Dynamic Convex Risk Measures

We develop an approach for solving time-consistent risk-sensitive stochastic optimization problems using model-free reinforcement learning (RL). Specifically, we assume agents assess the risk of a sequence of random variables using dynamic convex risk measures. We employ a time-consistent dynamic programming principle to determine the value of a particular policy, and develop policy gradient update rules. We further develop an actor-critic style algorithm using neural networks to optimize over policies. Finally, we demonstrate the performance and flexibility of our approach by applying it to optimization problems in statistical arbitrage trading and obstacle avoidance robot control.

Deep Learning for Principal-Agent Mean Field Games

Here, we develop a deep learning algorithm for solving Principal-Agent (PA) mean field games with market-clearing conditions -- a class of problems that have thus far not been studied and one that poses difficulties for standard numerical methods. We use an actor-critic approach to optimization, where the agents form a Nash equilibria according to the principal's penalty function, and the principal evaluates the resulting equilibria. The inner problem's Nash equilibria is obtained using a variant of the deep backward stochastic differential equation (BSDE) method modified for McKean-Vlasov forward-backward SDEs that includes dependence on the distribution over both the forward and backward processes. The outer problem's loss is further approximated by a neural net by sampling over the space of penalty functions. We apply our approach to a stylized PA problem arising in Renewable Energy Certificate (REC) markets, where agents may rent clean energy production capacity, trade RECs, and expand their long-term capacity to navigate the market at maximum profit. Our numerical results illustrate the efficacy of the algorithm and lead to interesting insights into the nature of optimal PA interactions in the mean-field limit of these markets.