Learning conditional distributions on continuous spaces

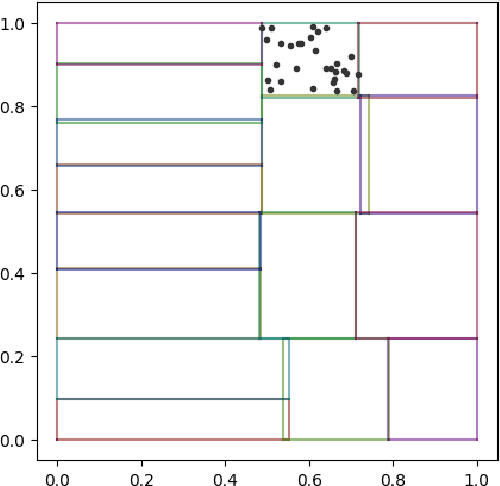
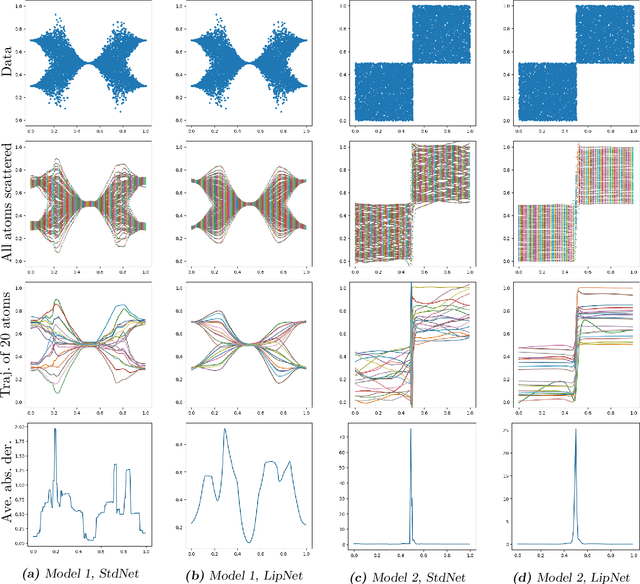
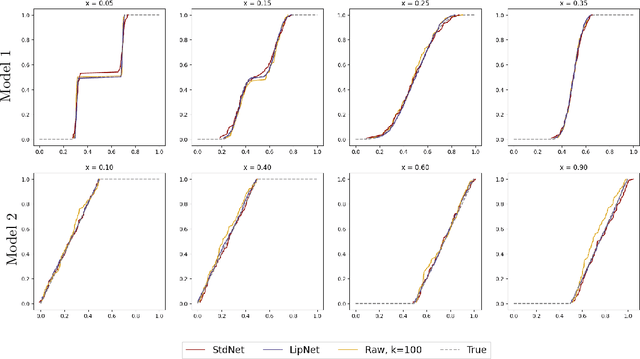
We investigate sample-based learning of conditional distributions on multi-dimensional unit boxes, allowing for different dimensions of the feature and target spaces. Our approach involves clustering data near varying query points in the feature space to create empirical measures in the target space. We employ two distinct clustering schemes: one based on a fixed-radius ball and the other on nearest neighbors. We establish upper bounds for the convergence rates of both methods and, from these bounds, deduce optimal configurations for the radius and the number of neighbors. We propose to incorporate the nearest neighbors method into neural network training, as our empirical analysis indicates it has better performance in practice. For efficiency, our training process utilizes approximate nearest neighbors search with random binary space partitioning. Additionally, we employ the Sinkhorn algorithm and a sparsity-enforced transport plan. Our empirical findings demonstrate that, with a suitably designed structure, the neural network has the ability to adapt to a suitable level of Lipschitz continuity locally. For reproducibility, our code is available at \url{https://github.com/zcheng-a/LCD_kNN}.

Eliciting Risk Aversion with Inverse Reinforcement Learning via Interactive Questioning

This paper proposes a novel framework for identifying an agent's risk aversion using interactive questioning. Our study is conducted in two scenarios: a one-period case and an infinite horizon case. In the one-period case, we assume that the agent's risk aversion is characterized by a cost function of the state and a distortion risk measure. In the infinite horizon case, we model risk aversion with an additional component, a discount factor. Assuming the access to a finite set of candidates containing the agent's true risk aversion, we show that asking the agent to demonstrate her optimal policies in various environment, which may depend on their previous answers, is an effective means of identifying the agent's risk aversion. Specifically, we prove that the agent's risk aversion can be identified as the number of questions tends to infinity, and the questions are randomly designed. We also develop an algorithm for designing optimal questions and provide empirical evidence that our method learns risk aversion significantly faster than randomly designed questions in simulations. Our framework has important applications in robo-advising and provides a new approach for identifying an agent's risk preferences.

Distributional Method for Risk Averse Reinforcement Learning

We introduce a distributional method for learning the optimal policy in risk averse Markov decision process with finite state action spaces, latent costs, and stationary dynamics. We assume sequential observations of states, actions, and costs and assess the performance of a policy using dynamic risk measures constructed from nested Kusuoka-type conditional risk mappings. For such performance criteria, randomized policies may outperform deterministic policies, therefore, the candidate policies lie in the d-dimensional simplex where d is the cardinality of the action space. Existing risk averse reinforcement learning methods seldom concern randomized policies, na\"ive extensions to current setting suffer from the curse of dimensionality. By exploiting certain structures embedded in the corresponding dynamic programming principle, we propose a distributional learning method for seeking the optimal policy. The conditional distribution of the value function is casted into a specific type of function, which is chosen with in mind the ease of risk averse optimization. We use a deep neural network to approximate said function, illustrate that the proposed method avoids the curse of dimensionality in the exploration phase, and explore the method's performance with a wide range of model parameters that are picked randomly.