Robust Reinforcement Learning with Dynamic Distortion Risk Measures

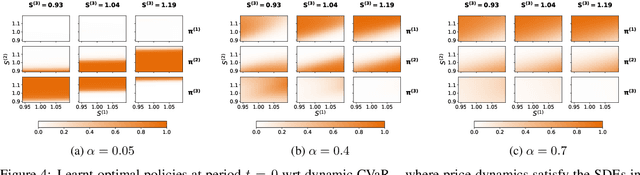
In a reinforcement learning (RL) setting, the agent's optimal strategy heavily depends on her risk preferences and the underlying model dynamics of the training environment. These two aspects influence the agent's ability to make well-informed and time-consistent decisions when facing testing environments. In this work, we devise a framework to solve robust risk-aware RL problems where we simultaneously account for environmental uncertainty and risk with a class of dynamic robust distortion risk measures. Robustness is introduced by considering all models within a Wasserstein ball around a reference model. We estimate such dynamic robust risk measures using neural networks by making use of strictly consistent scoring functions, derive policy gradient formulae using the quantile representation of distortion risk measures, and construct an actor-critic algorithm to solve this class of robust risk-aware RL problems. We demonstrate the performance of our algorithm on a portfolio allocation example.

Eliciting Risk Aversion with Inverse Reinforcement Learning via Interactive Questioning

This paper proposes a novel framework for identifying an agent's risk aversion using interactive questioning. Our study is conducted in two scenarios: a one-period case and an infinite horizon case. In the one-period case, we assume that the agent's risk aversion is characterized by a cost function of the state and a distortion risk measure. In the infinite horizon case, we model risk aversion with an additional component, a discount factor. Assuming the access to a finite set of candidates containing the agent's true risk aversion, we show that asking the agent to demonstrate her optimal policies in various environment, which may depend on their previous answers, is an effective means of identifying the agent's risk aversion. Specifically, we prove that the agent's risk aversion can be identified as the number of questions tends to infinity, and the questions are randomly designed. We also develop an algorithm for designing optimal questions and provide empirical evidence that our method learns risk aversion significantly faster than randomly designed questions in simulations. Our framework has important applications in robo-advising and provides a new approach for identifying an agent's risk preferences.

Conditionally Elicitable Dynamic Risk Measures for Deep Reinforcement Learning

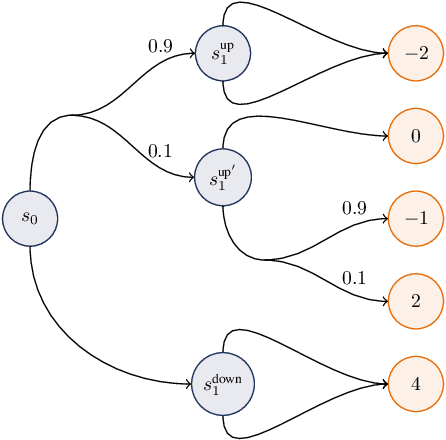
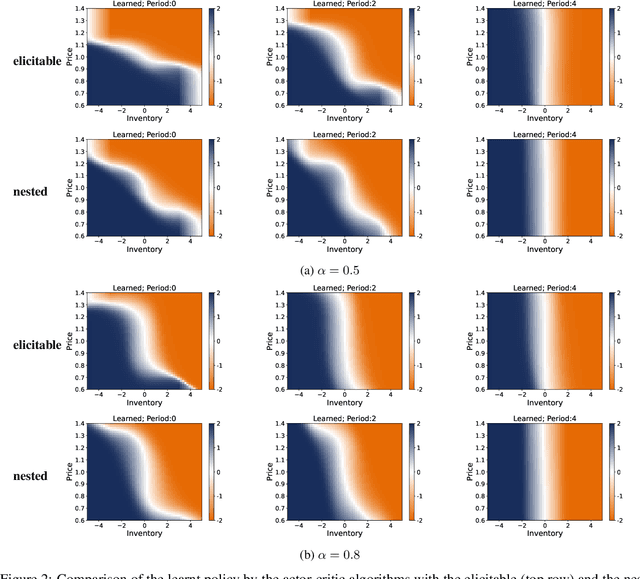
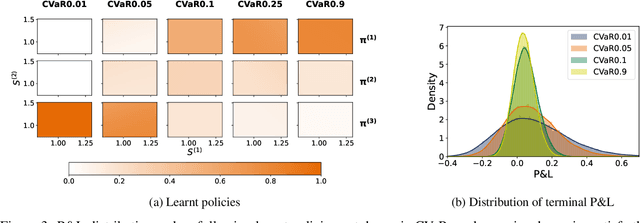
We propose a novel framework to solve risk-sensitive reinforcement learning (RL) problems where the agent optimises time-consistent dynamic spectral risk measures. Based on the notion of conditional elicitability, our methodology constructs (strictly consistent) scoring functions that are used as penalizers in the estimation procedure. Our contribution is threefold: we (i) devise an efficient approach to estimate a class of dynamic spectral risk measures with deep neural networks, (ii) prove that these dynamic spectral risk measures may be approximated to any arbitrary accuracy using deep neural networks, and (iii) develop a risk-sensitive actor-critic algorithm that uses full episodes and does not require any additional nested transitions. We compare our conceptually improved reinforcement learning algorithm with the nested simulation approach and illustrate its performance in two settings: statistical arbitrage and portfolio allocation on both simulated and real data.

Reinforcement Learning with Dynamic Convex Risk Measures

We develop an approach for solving time-consistent risk-sensitive stochastic optimization problems using model-free reinforcement learning (RL). Specifically, we assume agents assess the risk of a sequence of random variables using dynamic convex risk measures. We employ a time-consistent dynamic programming principle to determine the value of a particular policy, and develop policy gradient update rules. We further develop an actor-critic style algorithm using neural networks to optimize over policies. Finally, we demonstrate the performance and flexibility of our approach by applying it to optimization problems in statistical arbitrage trading and obstacle avoidance robot control.