Stabilizing Transformer Training Through Consensus

Standard attention-based transformers are known to exhibit instability under learning rate overspecification during training, particularly at high learning rates. While various methods have been proposed to improve resilience to such overspecification by modifying the optimization procedure, fundamental architectural innovations to this end remain underexplored. In this work, we illustrate that the consensus mechanism, a drop-in replacement for attention, stabilizes transformer training across a wider effective range of learning rates. We formulate consensus as a graphical model and provide extensive empirical analysis demonstrating improved stability across learning rate sweeps on text, DNA, and protein modalities. We further propose a hybrid consensus-attention framework that preserves performance while improving stability. We provide theoretical analysis characterizing the properties of consensus.

Score-Based Quickest Change Detection and Fault Identification for Multi-Stream Signals

This paper introduces an approach to multi-stream quickest change detection and fault isolation for unnormalized and score-based statistical models. Traditional optimal algorithms in the quickest change detection literature require explicit pre-change and post-change distributions to calculate the likelihood ratio of the observations, which can be computationally expensive for higher-dimensional data and sometimes even infeasible for complex machine learning models. To address these challenges, we propose the min-SCUSUM method, a Hyvarinen score-based algorithm that computes the difference of score functions in place of log-likelihood ratios. We provide a delay and false alarm analysis of the proposed algorithm, showing that its asymptotic performance depends on the Fisher divergence between the pre- and post-change distributions. Furthermore, we establish an upper bound on the probability of fault misidentification in distinguishing the affected stream from the unaffected ones.

Robust Score-Based Quickest Change Detection

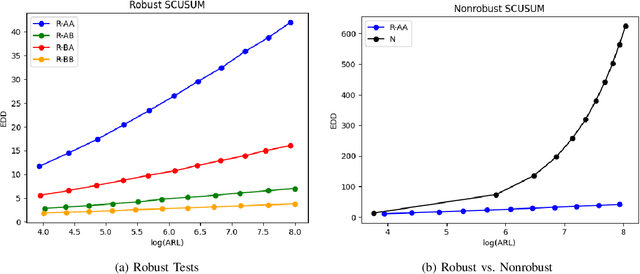
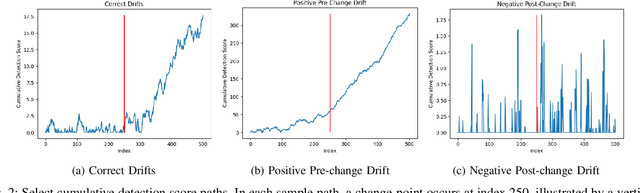
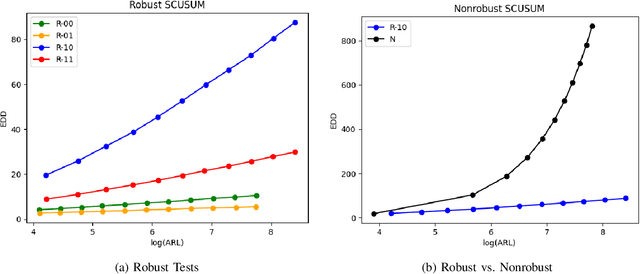
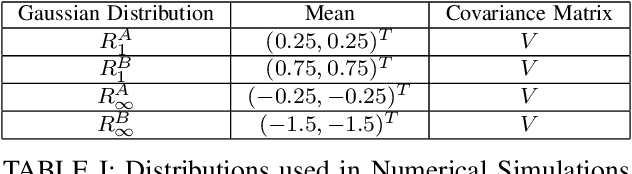
Methods in the field of quickest change detection rapidly detect in real-time a change in the data-generating distribution of an online data stream. Existing methods have been able to detect this change point when the densities of the pre- and post-change distributions are known. Recent work has extended these results to the case where the pre- and post-change distributions are known only by their score functions. This work considers the case where the pre- and post-change score functions are known only to correspond to distributions in two disjoint sets. This work employs a pair of "least-favorable" distributions to robustify the existing score-based quickest change detection algorithm, the properties of which are studied. This paper calculates the least-favorable distributions for specific model classes and provides methods of estimating the least-favorable distributions for common constructions. Simulation results are provided demonstrating the performance of our robust change detection algorithm.