Sarika Jalan
Estimation of Correlation Matrices from Limited time series Data using Machine Learning
Sep 02, 2022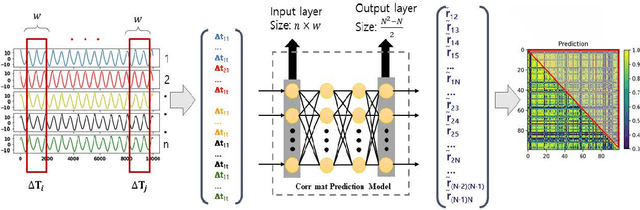

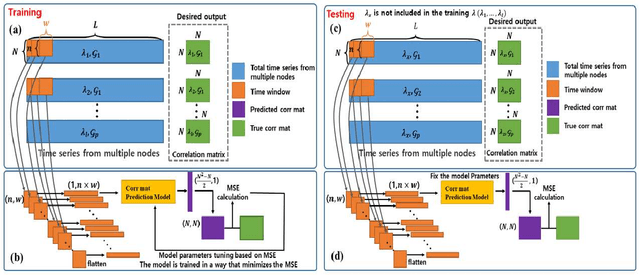
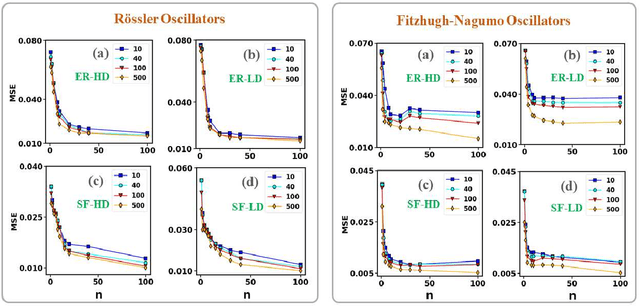
Abstract:Prediction of correlation matrices from given time series data has several applications for a range of problems, such as inferring neuronal connections from spiking data, deducing causal dependencies between genes from expression data, and discovering long spatial range influences in climate variations. Traditional methods of predicting correlation matrices utilize time series data of all the nodes of the underlying networks. Here, we use a supervised machine learning technique to predict the correlation matrix of entire systems from finite time series information of a few randomly selected nodes. The accuracy of the prediction from the model confirms that only a limited time series of a subset of the entire system is enough to make good correlation matrix predictions. Furthermore, using an unsupervised learning algorithm, we provide insights into the success of the predictions from our model. Finally, we apply the machine learning model developed here to real-world data sets.
Machine Learning assisted Chimera and Solitary states in Networks
Nov 02, 2020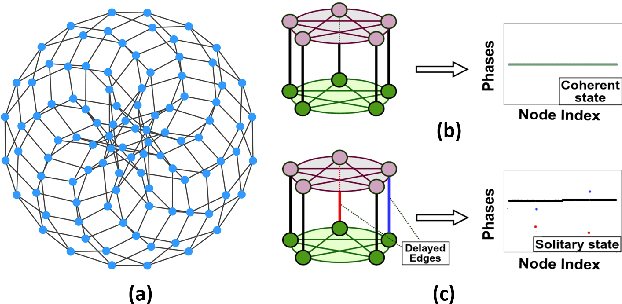
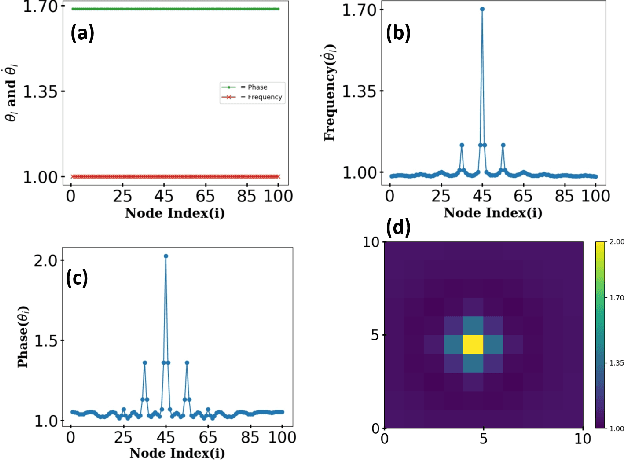
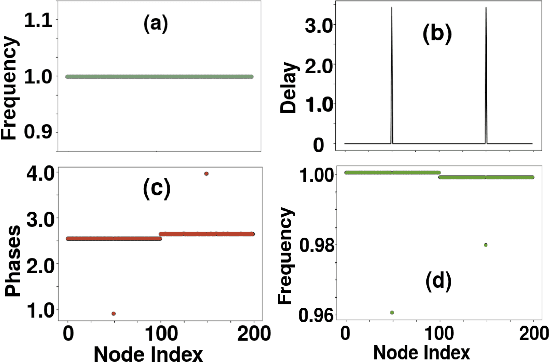
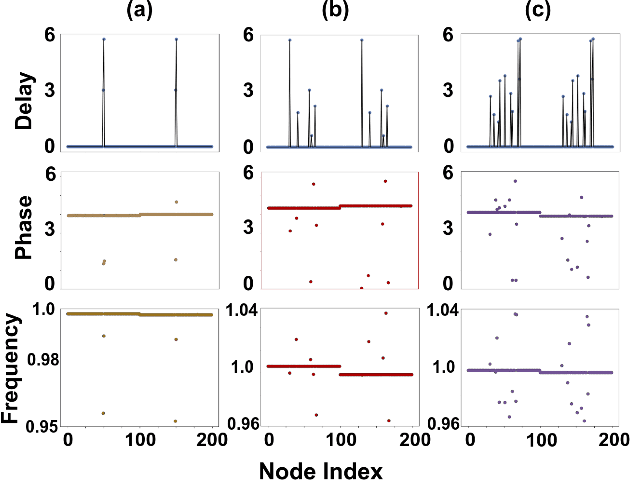
Abstract:Chimera and Solitary states have captivated scientists and engineers due to their peculiar dynamical states corresponding to co-existence of coherent and incoherent dynamical evolution in coupled units in various natural and artificial systems. It has been further demonstrated that such states can be engineered in systems of coupled oscillators by suitable implementation of communication delays. Here, using supervised machine learning, we predict (a) the precise value of delay which is sufficient for engineering chimera and solitary states for a given set of system's parameters, as well as (b) the intensity of incoherence for such engineered states. Ergo, using few initial data points we generate a machine learning model which can then create a more refined phase plot as well as by including new parameter values. We demonstrate our results for two different examples consisting of single layer and multi layer networks. First, the chimera states (solitary states) are engineered by establishing delays in the neighboring links of a node (the interlayer links) in a 2-D lattice (multiplex network) of oscillators. Then, different machine learning classifiers, KNN, SVM and MLP-Neural Network are employed by feeding the data obtained from the network models. Once a machine learning model is trained using the limited amount of data, it predicts the precise value of critical delay as well as the intensity of incoherence for a given unknown systems parameters values. Testing accuracy, sensitivity and specificity analysis reveal that MLP-NN classifier is better suited than Knn or SVM classifier for the predictions of parameters values for engineered chimera and solitary states. The technique provides an easy methodology to predict critical delay values as well as intensity of incoherence for that delay value for designing an experimental setup to create solitary and chimera states.
Identification of Chimera using Machine Learning
Jan 16, 2020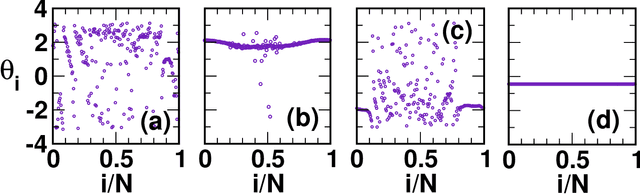

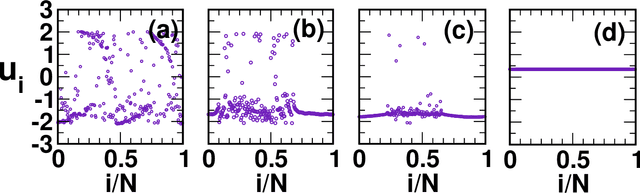
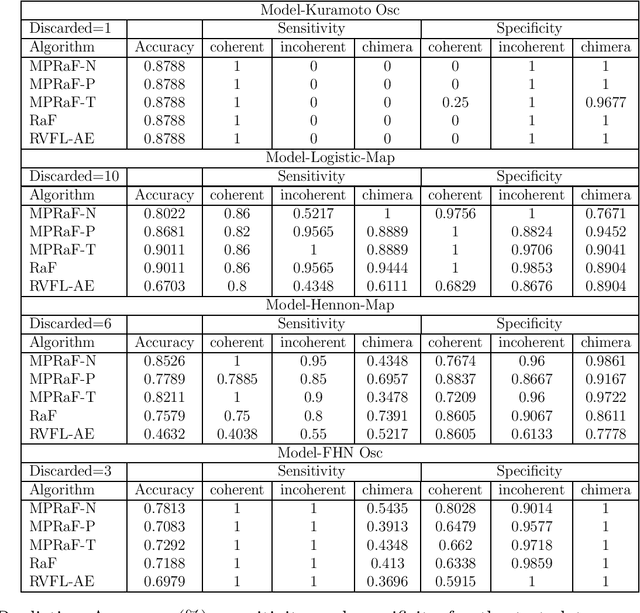
Abstract:Coupled dynamics on the network models have been tremendously helpful in getting insight into complex spatiotemporal dynamical patterns of a wide variety of large-scale real-world complex systems. Chimera, a state of coexistence of incoherence and coherence, is one of such patterns arising in identically coupled oscillators, which has recently drawn tremendous attention due to its peculiar nature and wide applicability, specially in neuroscience. The identification of chimera is a challenging problem due to ambiguity in its appearance. We present a distinctive approach to identify and characterize the chimera state using machine learning techniques, namely random forest, oblique random forests via multi-surface proximal support vector machines (MPRaF-T, P, N) and sparse pre-trained / auto-encoder based random vector functional link neural network (RVFL-AE). We demonstrate high accuracy in identifying the coherent, incoherent and chimera states from given spatial profiles. We validate this approach for different time-continuous and time discrete coupled dynamics on networks. This work provides a direction for employing machine learning techniques to identify dynamical patterns arising due to the interaction among non-linear units on large-scale, and for characterizing complex spatio-temporal phenomena in real-world systems for various applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge