Graph Neural Networks for Identifying Steady-State Behavior in Complex Networks

In complex systems, information propagation can be defined as diffused or delocalized, weakly localized, and strongly localized. Can a machine learning model learn the behavior of a linear dynamical system on networks? In this work, we develop a graph neural network framework for identifying the steady-state behavior of the linear dynamical system. We reveal that our model learns the different states with high accuracy. To understand the explainability of our model, we provide an analytical derivation for the forward and backward propagation of our framework. Finally, we use the real-world graphs in our model for validation.

Master Stability Functions in Complex Networks

Synchronization is an emergent phenomenon in coupled dynamical networks. The Master Stability Function (MSF) is a highly elegant and powerful tool for characterizing the stability of synchronization states. However, a significant challenge lies in determining the MSF for complex dynamical networks driven by nonlinear interaction mechanisms. These mechanisms introduce additional complexity through the intricate connectivity of interacting elements within the network and the intrinsic dynamics, which are governed by nonlinear processes with diverse parameters and higher dimensionality of systems. Over the past 25 years, extensive research has focused on determining the MSF for pairwise coupled identical systems with diffusive coupling. Our literature survey highlights two significant advancements in recent years: the consideration of multilayer networks instead of single-layer networks and the extension of MSF analysis to incorporate higher-order interactions alongside pairwise interactions. In this review article, we revisit the analysis of the MSF for diffusively pairwise coupled dynamical systems and extend this framework to more general coupling schemes. Furthermore, we systematically derive the MSF for multilayer dynamical networks and single-layer coupled systems by incorporating higher-order interactions alongside pairwise interactions. The primary focus of our review is on the analytical derivation and numerical computation of the MSF for complex dynamical networks. Finally, we demonstrate the application of the MSF in data science, emphasizing its relevance and potential in this rapidly evolving field.

Estimation of Correlation Matrices from Limited time series Data using Machine Learning

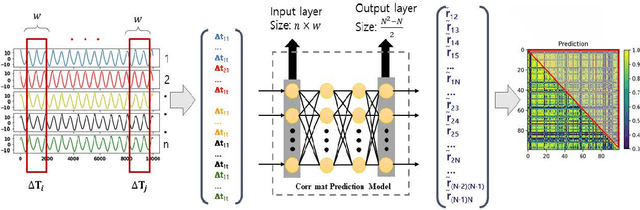
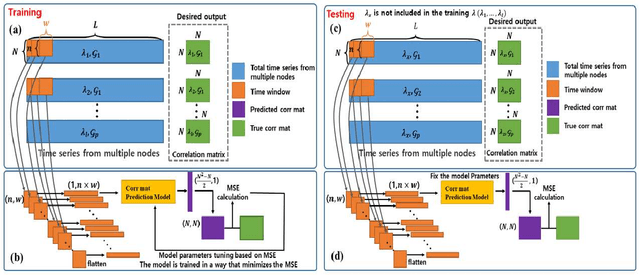
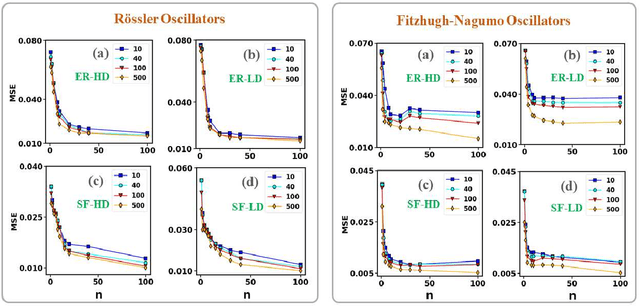
Prediction of correlation matrices from given time series data has several applications for a range of problems, such as inferring neuronal connections from spiking data, deducing causal dependencies between genes from expression data, and discovering long spatial range influences in climate variations. Traditional methods of predicting correlation matrices utilize time series data of all the nodes of the underlying networks. Here, we use a supervised machine learning technique to predict the correlation matrix of entire systems from finite time series information of a few randomly selected nodes. The accuracy of the prediction from the model confirms that only a limited time series of a subset of the entire system is enough to make good correlation matrix predictions. Furthermore, using an unsupervised learning algorithm, we provide insights into the success of the predictions from our model. Finally, we apply the machine learning model developed here to real-world data sets.