The Unintended Consequences of Discount Regularization: Improving Regularization in Certainty Equivalence Reinforcement Learning

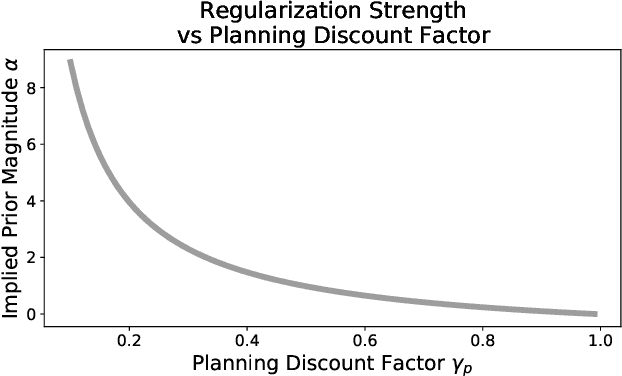
Discount regularization, using a shorter planning horizon when calculating the optimal policy, is a popular choice to restrict planning to a less complex set of policies when estimating an MDP from sparse or noisy data (Jiang et al., 2015). It is commonly understood that discount regularization functions by de-emphasizing or ignoring delayed effects. In this paper, we reveal an alternate view of discount regularization that exposes unintended consequences. We demonstrate that planning under a lower discount factor produces an identical optimal policy to planning using any prior on the transition matrix that has the same distribution for all states and actions. In fact, it functions like a prior with stronger regularization on state-action pairs with more transition data. This leads to poor performance when the transition matrix is estimated from data sets with uneven amounts of data across state-action pairs. Our equivalence theorem leads to an explicit formula to set regularization parameters locally for individual state-action pairs rather than globally. We demonstrate the failures of discount regularization and how we remedy them using our state-action-specific method across simple empirical examples as well as a medical cancer simulator.

Comparison and Unification of Three Regularization Methods in Batch Reinforcement Learning

In batch reinforcement learning, there can be poorly explored state-action pairs resulting in poorly learned, inaccurate models and poorly performing associated policies. Various regularization methods can mitigate the problem of learning overly-complex models in Markov decision processes (MDPs), however they operate in technically and intuitively distinct ways and lack a common form in which to compare them. This paper unifies three regularization methods in a common framework -- a weighted average transition matrix. Considering regularization methods in this common form illuminates how the MDP structure and the state-action pair distribution of the batch data set influence the relative performance of regularization methods. We confirm intuitions generated from the common framework by empirical evaluation across a range of MDPs and data collection policies.