Nickel and Diming Your GAN: A Dual-Method Approach to Enhancing GAN Efficiency via Knowledge Distillation

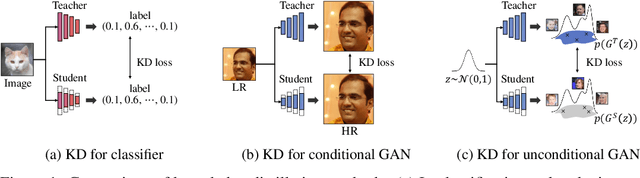
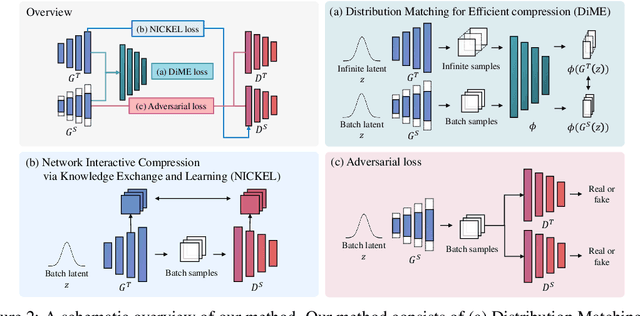
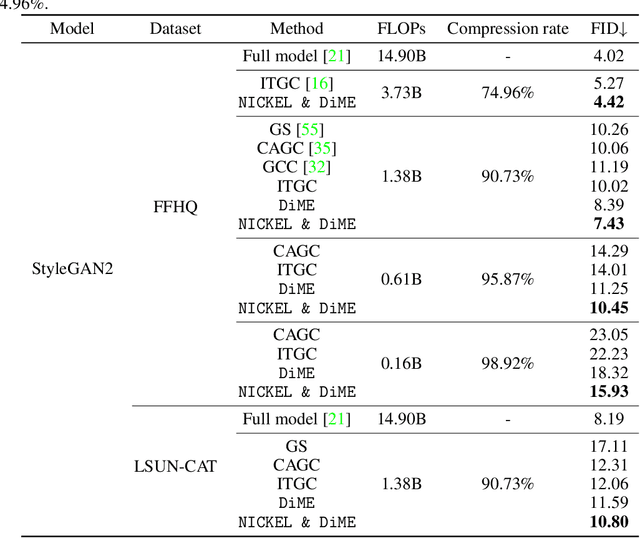
In this paper, we address the challenge of compressing generative adversarial networks (GANs) for deployment in resource-constrained environments by proposing two novel methodologies: Distribution Matching for Efficient compression (DiME) and Network Interactive Compression via Knowledge Exchange and Learning (NICKEL). DiME employs foundation models as embedding kernels for efficient distribution matching, leveraging maximum mean discrepancy to facilitate effective knowledge distillation. Simultaneously, NICKEL employs an interactive compression method that enhances the communication between the student generator and discriminator, achieving a balanced and stable compression process. Our comprehensive evaluation on the StyleGAN2 architecture with the FFHQ dataset shows the effectiveness of our approach, with NICKEL & DiME achieving FID scores of 10.45 and 15.93 at compression rates of 95.73% and 98.92%, respectively. Remarkably, our methods sustain generative quality even at an extreme compression rate of 99.69%, surpassing the previous state-of-the-art performance by a large margin. These findings not only demonstrate our methodologies' capacity to significantly lower GANs' computational demands but also pave the way for deploying high-quality GAN models in settings with limited resources. Our code will be released soon.

Can We Find Strong Lottery Tickets in Generative Models?

Yes. In this paper, we investigate strong lottery tickets in generative models, the subnetworks that achieve good generative performance without any weight update. Neural network pruning is considered the main cornerstone of model compression for reducing the costs of computation and memory. Unfortunately, pruning a generative model has not been extensively explored, and all existing pruning algorithms suffer from excessive weight-training costs, performance degradation, limited generalizability, or complicated training. To address these problems, we propose to find a strong lottery ticket via moment-matching scores. Our experimental results show that the discovered subnetwork can perform similarly or better than the trained dense model even when only 10% of the weights remain. To the best of our knowledge, we are the first to show the existence of strong lottery tickets in generative models and provide an algorithm to find it stably. Our code and supplementary materials are publicly available.