SPRIGHT: A Fast and Robust Framework for Sparse Walsh-Hadamard Transform

We consider the problem of computing the Walsh-Hadamard Transform (WHT) of some $N$-length input vector in the presence of noise, where the $N$-point Walsh spectrum is $K$-sparse with $K = {O}(N^{\delta})$ scaling sub-linearly in the input dimension $N$ for some $0<\delta<1$. Over the past decade, there has been a resurgence in research related to the computation of Discrete Fourier Transform (DFT) for some length-$N$ input signal that has a $K$-sparse Fourier spectrum. In particular, through a sparse-graph code design, our earlier work on the Fast Fourier Aliasing-based Sparse Transform (FFAST) algorithm computes the $K$-sparse DFT in time ${O}(K\log K)$ by taking ${O}(K)$ noiseless samples. Inspired by the coding-theoretic design framework, Scheibler et al. proposed the Sparse Fast Hadamard Transform (SparseFHT) algorithm that elegantly computes the $K$-sparse WHT in the absence of noise using ${O}(K\log N)$ samples in time ${O}(K\log^2 N)$. However, the SparseFHT algorithm explicitly exploits the noiseless nature of the problem, and is not equipped to deal with scenarios where the observations are corrupted by noise. Therefore, a question of critical interest is whether this coding-theoretic framework can be made robust to noise. Further, if the answer is yes, what is the extra price that needs to be paid for being robust to noise? In this paper, we show, quite interestingly, that there is {\it no extra price} that needs to be paid for being robust to noise other than a constant factor. In other words, we can maintain the same sample complexity ${O}(K\log N)$ and the computational complexity ${O}(K\log^2 N)$ as those of the noiseless case, using our SParse Robust Iterative Graph-based Hadamard Transform (SPRIGHT) algorithm.

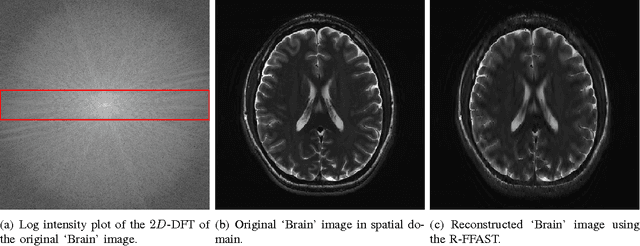
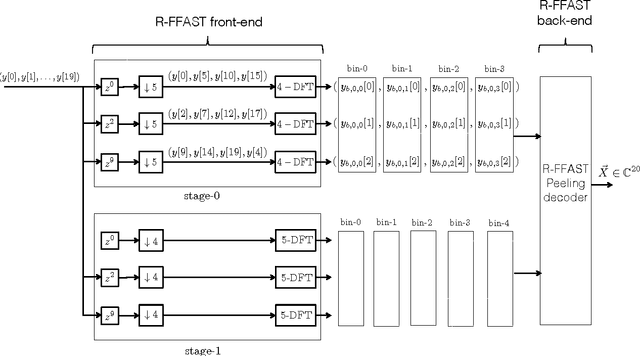
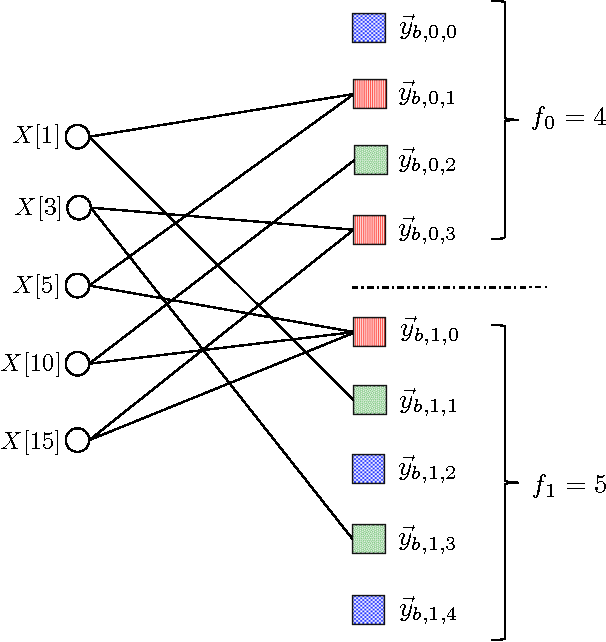
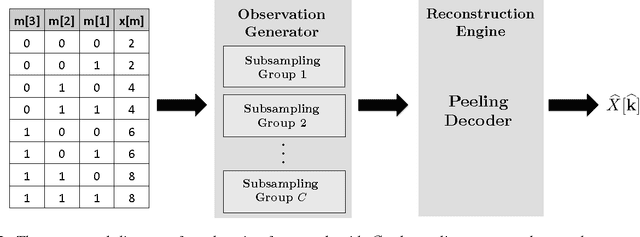
A robust sub-linear time R-FFAST algorithm for computing a sparse DFT

The Fast Fourier Transform (FFT) is the most efficiently known way to compute the Discrete Fourier Transform (DFT) of an arbitrary n-length signal, and has a computational complexity of O(n log n). If the DFT X of the signal x has only k non-zero coefficients (where k < n), can we do better? In [1], we addressed this question and presented a novel FFAST (Fast Fourier Aliasing-based Sparse Transform) algorithm that cleverly induces sparse graph alias codes in the DFT domain, via a Chinese-Remainder-Theorem (CRT)-guided sub-sampling operation of the time-domain samples. The resulting sparse graph alias codes are then exploited to devise a fast and iterative onion-peeling style decoder that computes an n length DFT of a signal using only O(k) time-domain samples and O(klog k) computations. The FFAST algorithm is applicable whenever k is sub-linear in n (i.e. k = o(n)), but is obviously most attractive when k is much smaller than n. In this paper, we adapt the FFAST framework of [1] to the case where the time-domain samples are corrupted by a white Gaussian noise. In particular, we show that the extended noise robust algorithm R-FFAST computes an n-length k-sparse DFT X using O(klog ^3 n) noise-corrupted time-domain samples, in O(klog^4n) computations, i.e., sub-linear time complexity. While our theoretical results are for signals with a uniformly random support of the non-zero DFT coefficients and additive white Gaussian noise, we provide simulation results which demonstrates that the R-FFAST algorithm performs well even for signals like MR images, that have an approximately sparse Fourier spectrum with a non-uniform support for the dominant DFT coefficients.