A robust sub-linear time R-FFAST algorithm for computing a sparse DFT
Paper and Code
Jan 01, 2015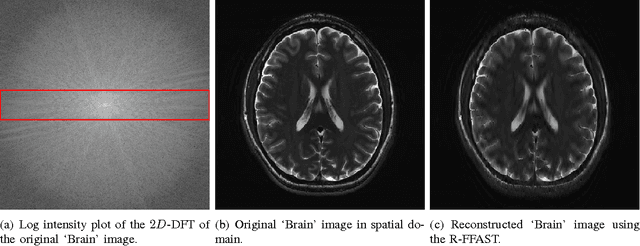
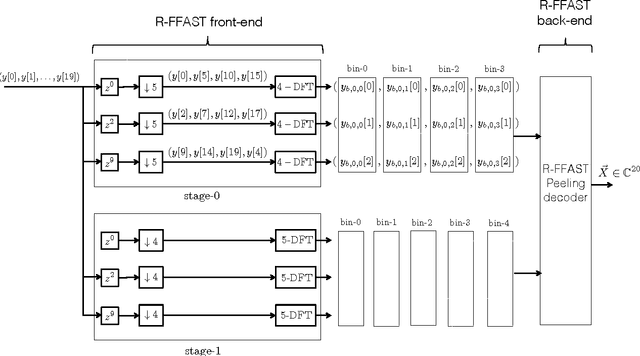
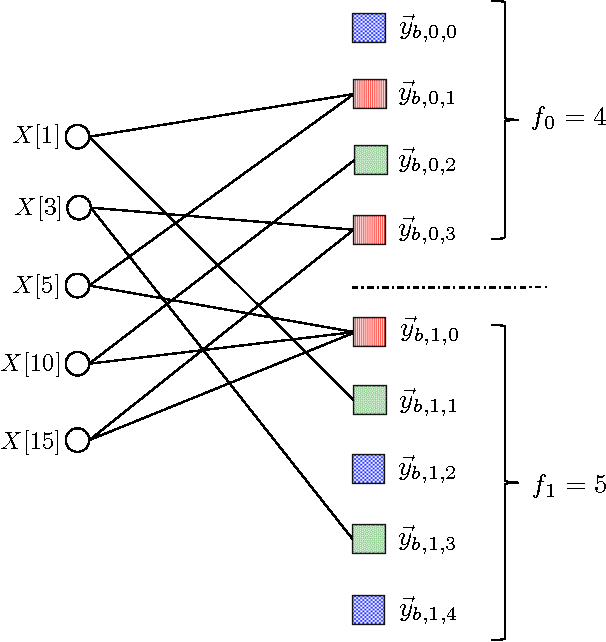
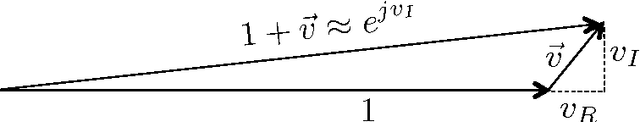
The Fast Fourier Transform (FFT) is the most efficiently known way to compute the Discrete Fourier Transform (DFT) of an arbitrary n-length signal, and has a computational complexity of O(n log n). If the DFT X of the signal x has only k non-zero coefficients (where k < n), can we do better? In [1], we addressed this question and presented a novel FFAST (Fast Fourier Aliasing-based Sparse Transform) algorithm that cleverly induces sparse graph alias codes in the DFT domain, via a Chinese-Remainder-Theorem (CRT)-guided sub-sampling operation of the time-domain samples. The resulting sparse graph alias codes are then exploited to devise a fast and iterative onion-peeling style decoder that computes an n length DFT of a signal using only O(k) time-domain samples and O(klog k) computations. The FFAST algorithm is applicable whenever k is sub-linear in n (i.e. k = o(n)), but is obviously most attractive when k is much smaller than n. In this paper, we adapt the FFAST framework of [1] to the case where the time-domain samples are corrupted by a white Gaussian noise. In particular, we show that the extended noise robust algorithm R-FFAST computes an n-length k-sparse DFT X using O(klog ^3 n) noise-corrupted time-domain samples, in O(klog^4n) computations, i.e., sub-linear time complexity. While our theoretical results are for signals with a uniformly random support of the non-zero DFT coefficients and additive white Gaussian noise, we provide simulation results which demonstrates that the R-FFAST algorithm performs well even for signals like MR images, that have an approximately sparse Fourier spectrum with a non-uniform support for the dominant DFT coefficients.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge