Active Sequential Posterior Estimation for Sample-Efficient Simulation-Based Inference

Computer simulations have long presented the exciting possibility of scientific insight into complex real-world processes. Despite the power of modern computing, however, it remains challenging to systematically perform inference under simulation models. This has led to the rise of simulation-based inference (SBI), a class of machine learning-enabled techniques for approaching inverse problems with stochastic simulators. Many such methods, however, require large numbers of simulation samples and face difficulty scaling to high-dimensional settings, often making inference prohibitive under resource-intensive simulators. To mitigate these drawbacks, we introduce active sequential neural posterior estimation (ASNPE). ASNPE brings an active learning scheme into the inference loop to estimate the utility of simulation parameter candidates to the underlying probabilistic model. The proposed acquisition scheme is easily integrated into existing posterior estimation pipelines, allowing for improved sample efficiency with low computational overhead. We further demonstrate the effectiveness of the proposed method in the travel demand calibration setting, a high-dimensional inverse problem commonly requiring computationally expensive traffic simulators. Our method outperforms well-tuned benchmarks and state-of-the-art posterior estimation methods on a large-scale real-world traffic network, as well as demonstrates a performance advantage over non-active counterparts on a suite of SBI benchmark environments.

When Physics Meets Machine Learning: A Survey of Physics-Informed Machine Learning

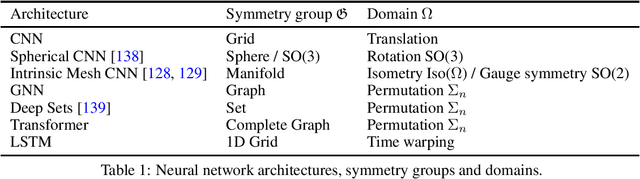
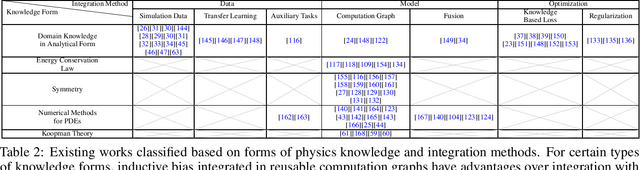
Physics-informed machine learning (PIML), referring to the combination of prior knowledge of physics, which is the high level abstraction of natural phenomenons and human behaviours in the long history, with data-driven machine learning models, has emerged as an effective way to mitigate the shortage of training data, to increase models' generalizability and to ensure the physical plausibility of results. In this paper, we survey an abundant number of recent works in PIML and summarize them from three aspects: (1) motivations of PIML, (2) physics knowledge in PIML, (3) methods of physics knowledge integration in PIML. We also discuss current challenges and corresponding research opportunities in PIML.