Empirical Optimal Transport between Conditional Distributions

Given samples from two joint distributions, we consider the problem of Optimal Transportation (OT) between the corresponding distributions conditioned on a common variable. The objective of this work is to estimate the associated transport cost (Wasserstein distance) as well as the transport plan between the conditionals as a function of the conditioned value. Since matching conditional distributions is at the core of supervised training of discriminative models and (implicit) conditional-generative models, OT between conditionals has the potential to be employed in diverse machine learning applications. However, since the conditionals involved in OT are implicitly specified via the joint samples, it is challenging to formulate this problem, especially when (i) the variable conditioned on is continuous and (ii) the marginal of this variable in the two distributions is different. We overcome these challenges by employing a specific kernel MMD (Maximum Mean Discrepancy) based regularizer that ensures the marginals of our conditional transport plan are close to the conditionals specified via the given joint samples. Under mild conditions, we prove that our estimator for this regularized transport cost is statistically consistent and derive finite-sample bounds on the estimation error. Application-specific details for parameterizing our conditional transport plan are also presented. Furthermore, we empirically evaluate our methodology on benchmark datasets in applications like classification, prompt learning for few-shot classification, and conditional-generation in the context of predicting cell responses to cancer treatment.

Improving Attribution Methods by Learning Submodular Functions

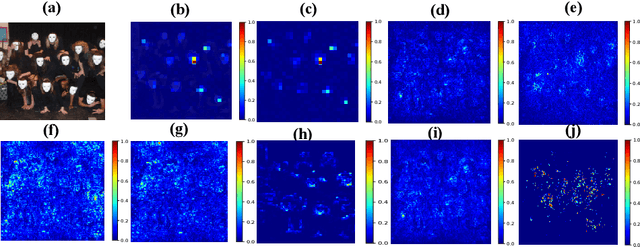
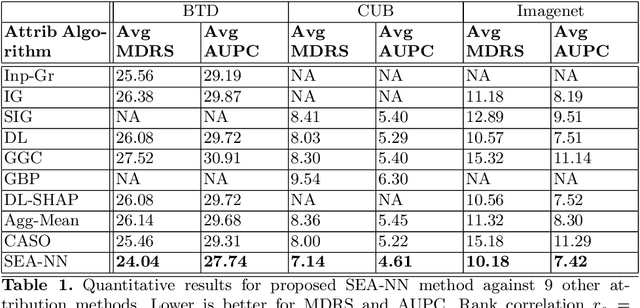
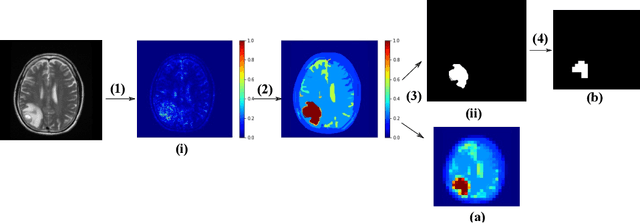
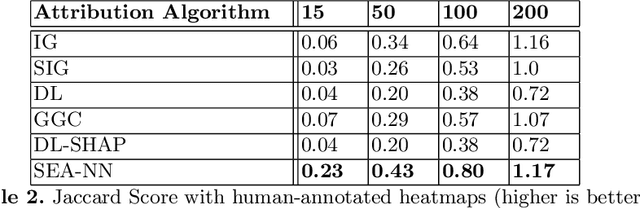
This work explores the novel idea of learning a submodular scoring function to improve the specificity/selectivity of existing feature attribution methods. Submodular scores are natural for attribution as they are known to accurately model the principle of diminishing returns. A new formulation for learning a deep submodular set function that is consistent with the real-valued attribution maps obtained by existing attribution methods is proposed. This formulation not only ensures that the scores for the heat maps that include the highly attributed features across the existing methods are high, but also that the score saturates even for the most specific heat map. The final attribution value of a feature is then defined as the marginal gain in the induced submodular score of the feature in the context of other highly attributed features, thus decreasing the attribution of redundant yet discriminatory features. Experiments on multiple datasets illustrate that the proposed attribution method achieves higher specificity while not degrading the discriminative power.