Trajectory Supervision for Continual Tool-Use Learning in LLMs

Most language-model training data shows final artifacts, not the process that produced them. We study a tractable version of this question in tool use: when a model learns a stream of new API domains, does keeping tool-use trajectories help compared with stripping the intermediate API trace? We fine-tune Llama 3.1 8B Instruct with QLoRA on API-Bank using four sequential domain blocks. Condition A strips previous API request/response lines from the prompt and trains the model to predict the next API call. Condition B keeps the trajectory context. In a single-seed pilot, full held-out generation evaluation shows that Condition B reaches 56.9\% final exact full-call accuracy compared with 39.2\% for Condition A. B also improves final API-name accuracy by 7.7 points. However, B uses 25.1\% more training tokens, the run uses one seed, and the task is next-call prediction rather than full dialogue success.

Dual-Track CoT: Budget-Aware Stepwise Guidance for Small LMs

Large Language Models (LLMs) solve many reasoning tasks via chain-of-thought (CoT) prompting, but smaller models (about 7 to 8B parameters) still struggle with multi-step reasoning under tight compute and token budgets. Existing test time reasoning methods such as self consistency (sampling multiple rationales and voting), Tree-of-Thoughts (search over intermediate thoughts), and critique revise loops improve performance, but often at high token cost and without fine-grained step-level control. This project1 aims to address that gap: can Small Language Models (SLMs) reason reliably using the same or fewer tokens? This question is both scientific and practical. Scientifically, it probes whether process supervision and simple test-time controls (such as token budgets and rejection of redundant steps) can substitute for model scale or large sampling counts. Practically, many deployments (on-device, low-latency, or cost-constrained settings) cannot afford huge models or dozens of sampled rationales per query. A method that improves SLM reasoning at fixed cost would therefore be directly useful.

The Quantum Learning Menagerie (A survey on Quantum learning for Classical concepts)

This paper surveys various results in the field of Quantum Learning theory, specifically focusing on learning quantum-encoded classical concepts in the Probably Approximately Correct (PAC) framework. The cornerstone of this work is the emphasis on query, sample, and time complexity separations between classical and quantum learning that emerge under learning with query access to different labeling oracles. This paper aims to consolidate all known results in the area under the above umbrella and underscore the limits of our understanding by leaving the reader with 23 open problems.

Generalization Bounds for Dependent Data using Online-to-Batch Conversion

In this work, we give generalization bounds of statistical learning algorithms trained on samples drawn from a dependent data source, both in expectation and with high probability, using the Online-to-Batch conversion paradigm. We show that the generalization error of statistical learners in the dependent data setting is equivalent to the generalization error of statistical learners in the i.i.d. setting up to a term that depends on the decay rate of the underlying mixing stochastic process and is independent of the complexity of the statistical learner. Our proof techniques involve defining a new notion of stability of online learning algorithms based on Wasserstein distances and employing "near-martingale" concentration bounds for dependent random variables to arrive at appropriate upper bounds for the generalization error of statistical learners trained on dependent data.

Quantum Solutions to the Privacy vs. Utility Tradeoff

In this work, we propose a novel architecture (and several variants thereof) based on quantum cryptographic primitives with provable privacy and security guarantees regarding membership inference attacks on generative models. Our architecture can be used on top of any existing classical or quantum generative models. We argue that the use of quantum gates associated with unitary operators provides inherent advantages compared to standard Differential Privacy based techniques for establishing guaranteed security from all polynomial-time adversaries.

Efficient Quantum Agnostic Improper Learning of Decision Trees

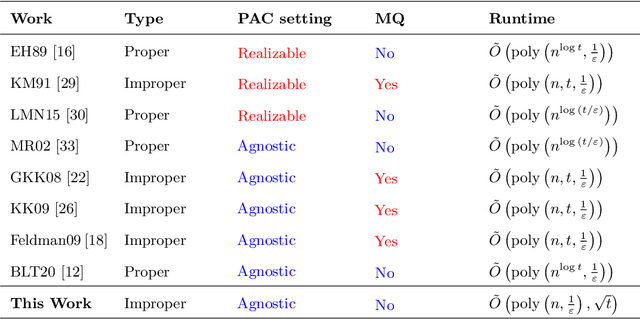
The agnostic setting is the hardest generalization of the PAC model since it is akin to learning with adversarial noise. We study an open question on the existence of efficient quantum boosting algorithms in this setting. We answer this question in the affirmative by providing a quantum version of the Kalai-Kanade potential boosting algorithm. This algorithm shows the standard quadratic speedup in the VC dimension of the weak learner compared to the classical case. Using our boosting algorithm as a subroutine, we give a quantum algorithm for agnostically learning decision trees in polynomial running time without using membership queries. To the best of our knowledge, this is the first algorithm (quantum or classical) to do so. Learning decision trees without membership queries is hard (and an open problem) in the standard classical realizable setting. In general, even coming up with weak learners in the agnostic setting is a challenging task. We show how to construct a quantum agnostic weak learner using standard quantum algorithms, which is of independent interest for designing ensemble learning setups.

Quantum Boosting using Domain-Partitioning Hypotheses

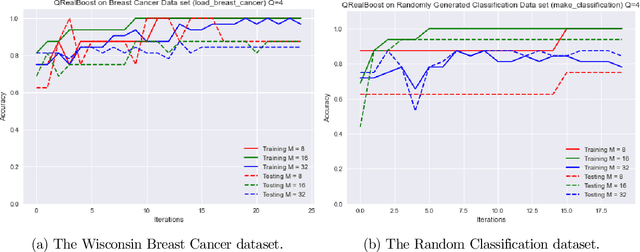
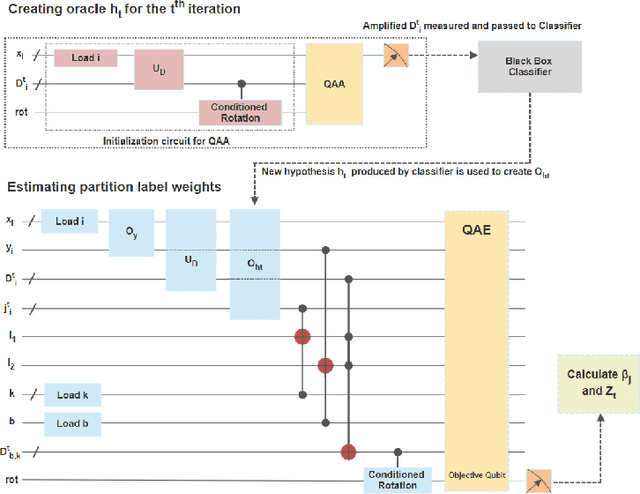
Boosting is an ensemble learning method that converts a weak learner into a strong learner in the PAC learning framework. Freund and Schapire gave the first classical boosting algorithm for binary hypothesis known as AdaBoost, and this was recently adapted into a quantum boosting algorithm by Arunachalam et al. Their quantum boosting algorithm (which we refer to as Q-AdaBoost) is quadratically faster than the classical version in terms of the VC-dimension of the hypothesis class of the weak learner but polynomially worse in the bias of the weak learner. In this work we design a different quantum boosting algorithm that uses domain partitioning hypotheses that are significantly more flexible than those used in prior quantum boosting algorithms in terms of margin calculations. Our algorithm Q-RealBoost is inspired by the "Real AdaBoost" (aka. RealBoost) extension to the original AdaBoost algorithm. Further, we show that Q-RealBoost provides a polynomial speedup over Q-AdaBoost in terms of both the bias of the weak learner and the time taken by the weak learner to learn the target concept class.