Efficient Quantum Agnostic Improper Learning of Decision Trees

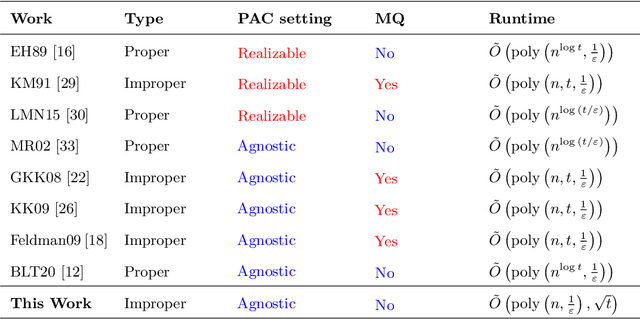
The agnostic setting is the hardest generalization of the PAC model since it is akin to learning with adversarial noise. We study an open question on the existence of efficient quantum boosting algorithms in this setting. We answer this question in the affirmative by providing a quantum version of the Kalai-Kanade potential boosting algorithm. This algorithm shows the standard quadratic speedup in the VC dimension of the weak learner compared to the classical case. Using our boosting algorithm as a subroutine, we give a quantum algorithm for agnostically learning decision trees in polynomial running time without using membership queries. To the best of our knowledge, this is the first algorithm (quantum or classical) to do so. Learning decision trees without membership queries is hard (and an open problem) in the standard classical realizable setting. In general, even coming up with weak learners in the agnostic setting is a challenging task. We show how to construct a quantum agnostic weak learner using standard quantum algorithms, which is of independent interest for designing ensemble learning setups.

Dimensionality Reduction for Categorical Data

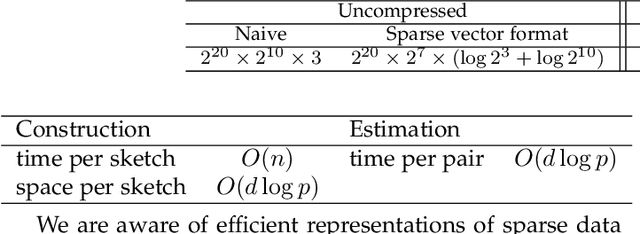
Categorical attributes are those that can take a discrete set of values, e.g., colours. This work is about compressing vectors over categorical attributes to low-dimension discrete vectors. The current hash-based methods compressing vectors over categorical attributes to low-dimension discrete vectors do not provide any guarantee on the Hamming distances between the compressed representations. Here we present FSketch to create sketches for sparse categorical data and an estimator to estimate the pairwise Hamming distances among the uncompressed data only from their sketches. We claim that these sketches can be used in the usual data mining tasks in place of the original data without compromising the quality of the task. For that, we ensure that the sketches also are categorical, sparse, and the Hamming distance estimates are reasonably precise. Both the sketch construction and the Hamming distance estimation algorithms require just a single-pass; furthermore, changes to a data point can be incorporated into its sketch in an efficient manner. The compressibility depends upon how sparse the data is and is independent of the original dimension -- making our algorithm attractive for many real-life scenarios. Our claims are backed by rigorous theoretical analysis of the properties of FSketch and supplemented by extensive comparative evaluations with related algorithms on some real-world datasets. We show that FSketch is significantly faster, and the accuracy obtained by using its sketches are among the top for the standard unsupervised tasks of RMSE, clustering and similarity search.

Efficient Binary Embedding of Categorical Data using BinSketch

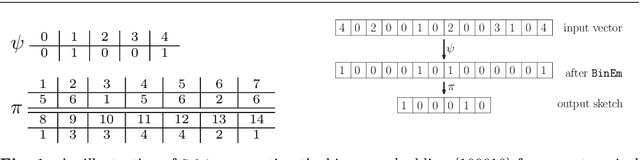
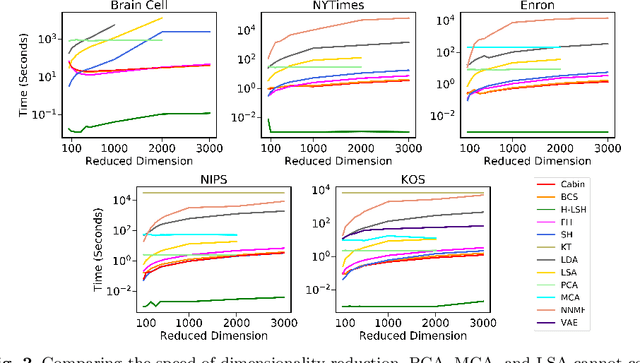
In this work, we present a dimensionality reduction algorithm, aka. sketching, for categorical datasets. Our proposed sketching algorithm Cabin constructs low-dimensional binary sketches from high-dimensional categorical vectors, and our distance estimation algorithm Cham computes a close approximation of the Hamming distance between any two original vectors only from their sketches. The minimum dimension of the sketches required by Cham to ensure a good estimation theoretically depends only on the sparsity of the data points - making it useful for many real-life scenarios involving sparse datasets. We present a rigorous theoretical analysis of our approach and supplement it with extensive experiments on several high-dimensional real-world data sets, including one with over a million dimensions. We show that the Cabin and Cham duo is a significantly fast and accurate approach for tasks such as RMSE, all-pairs similarity, and clustering when compared to working with the full dataset and other dimensionality reduction techniques.

Quantum Boosting using Domain-Partitioning Hypotheses

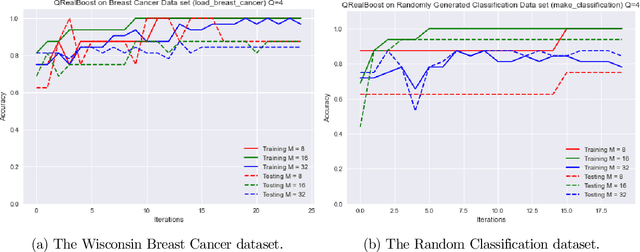
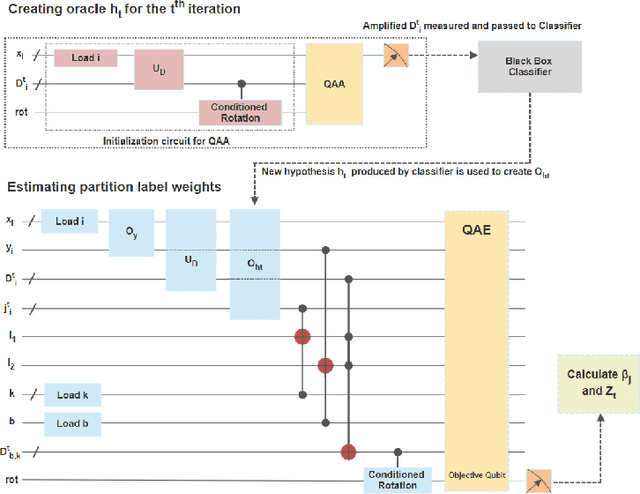
Boosting is an ensemble learning method that converts a weak learner into a strong learner in the PAC learning framework. Freund and Schapire gave the first classical boosting algorithm for binary hypothesis known as AdaBoost, and this was recently adapted into a quantum boosting algorithm by Arunachalam et al. Their quantum boosting algorithm (which we refer to as Q-AdaBoost) is quadratically faster than the classical version in terms of the VC-dimension of the hypothesis class of the weak learner but polynomially worse in the bias of the weak learner. In this work we design a different quantum boosting algorithm that uses domain partitioning hypotheses that are significantly more flexible than those used in prior quantum boosting algorithms in terms of margin calculations. Our algorithm Q-RealBoost is inspired by the "Real AdaBoost" (aka. RealBoost) extension to the original AdaBoost algorithm. Further, we show that Q-RealBoost provides a polynomial speedup over Q-AdaBoost in terms of both the bias of the weak learner and the time taken by the weak learner to learn the target concept class.

QUINT: Node embedding using network hashing

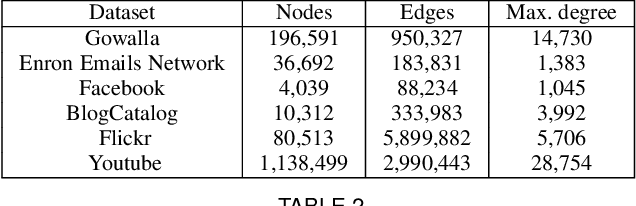
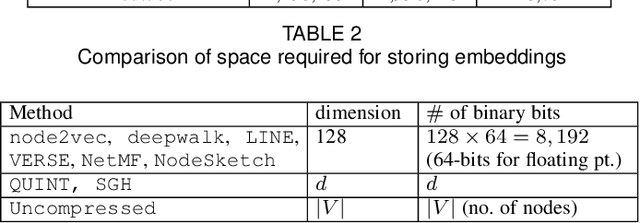
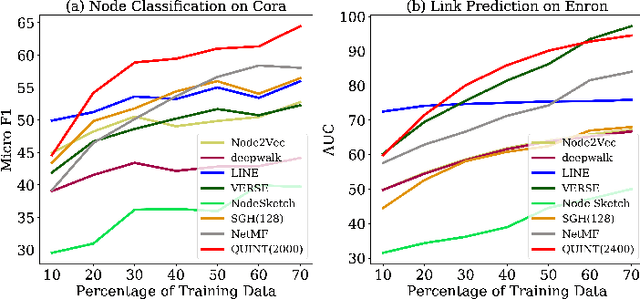
Representation learning using network embedding has received tremendous attention due to its efficacy to solve downstream tasks. Popular embedding methods (such as deepwalk, node2vec, LINE) are based on a neural architecture, thus unable to scale on large networks both in terms of time and space usage. Recently, we proposed BinSketch, a sketching technique for compressing binary vectors to binary vectors. In this paper, we show how to extend BinSketch and use it for network hashing. Our proposal named QUINT is built upon BinSketch, and it embeds nodes of a sparse network onto a low-dimensional space using simple bi-wise operations. QUINT is the first of its kind that provides tremendous gain in terms of speed and space usage without compromising much on the accuracy of the downstream tasks. Extensive experiments are conducted to compare QUINT with seven state-of-the-art network embedding methods for two end tasks - link prediction and node classification. We observe huge performance gain for QUINT in terms of speedup (up to 7000x) and space saving (up to 80x) due to its bit-wise nature to obtain node embedding. Moreover, QUINT is a consistent top-performer for both the tasks among the baselines across all the datasets. Our empirical observations are backed by rigorous theoretical analysis to justify the effectiveness of QUINT. In particular, we prove that QUINT retains enough structural information which can be used further to approximate many topological properties of networks with high confidence.

Efficient Sketching Algorithm for Sparse Binary Data

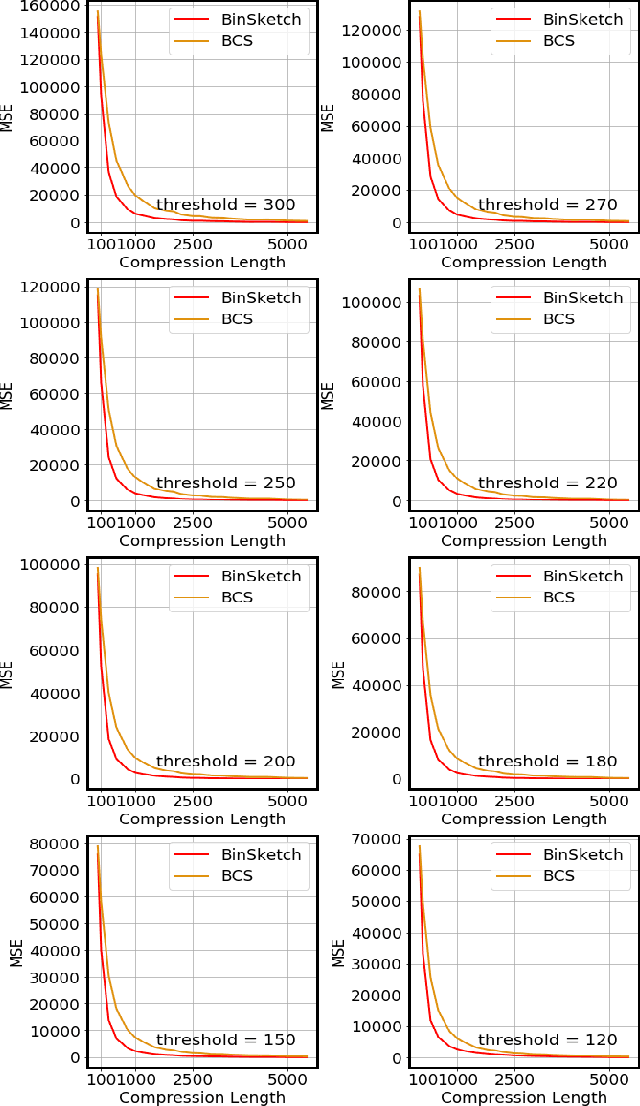
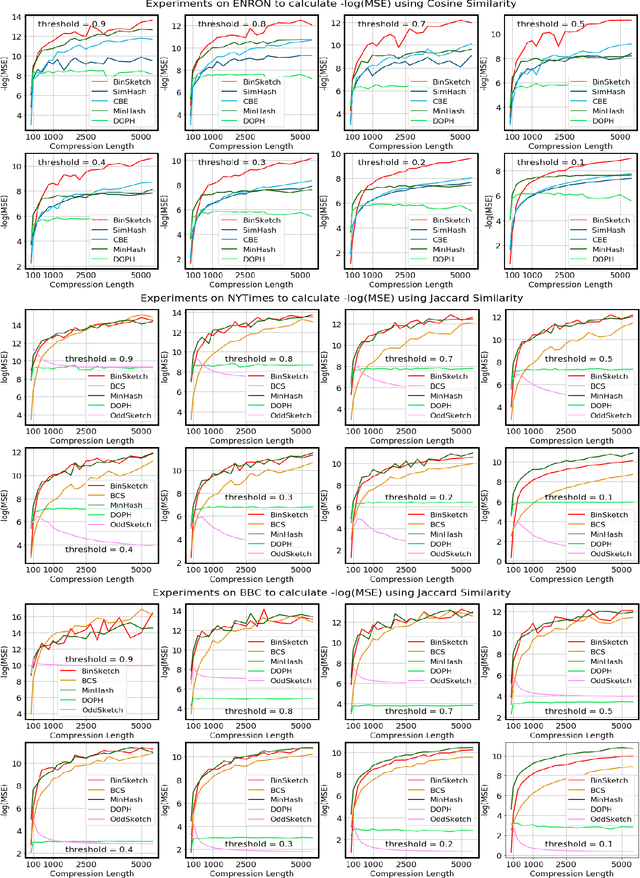
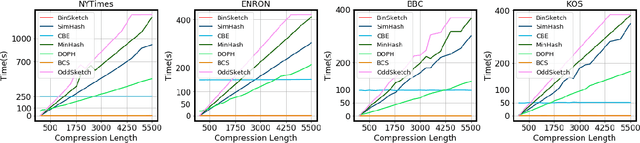
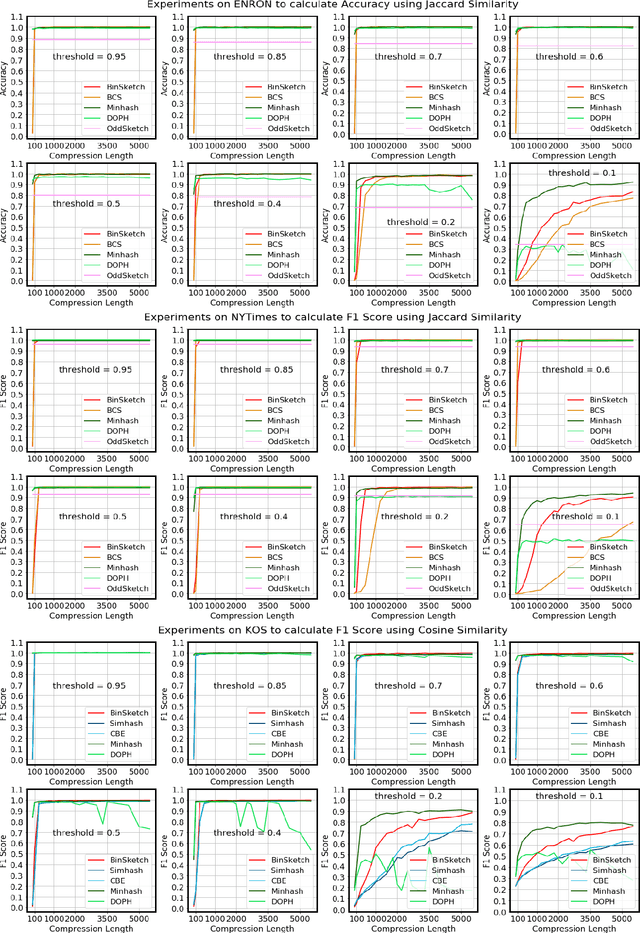
Recent advancement of the WWW, IOT, social network, e-commerce, etc. have generated a large volume of data. These datasets are mostly represented by high dimensional and sparse datasets. Many fundamental subroutines of common data analytic tasks such as clustering, classification, ranking, nearest neighbour search, etc. scale poorly with the dimension of the dataset. In this work, we address this problem and propose a sketching (alternatively, dimensionality reduction) algorithm -- $\binsketch$ (Binary Data Sketch) -- for sparse binary datasets. $\binsketch$ preserves the binary version of the dataset after sketching and maintains estimates for multiple similarity measures such as Jaccard, Cosine, Inner-Product similarities, and Hamming distance, on the same sketch. We present a theoretical analysis of our algorithm and complement it with extensive experimentation on several real-world datasets. We compare the performance of our algorithm with the state-of-the-art algorithms on the task of mean-square-error and ranking. Our proposed algorithm offers a comparable accuracy while suggesting a significant speedup in the dimensionality reduction time, with respect to the other candidate algorithms. Our proposal is simple, easy to implement, and therefore can be adopted in practice.