Generalization Bounds for Dependent Data using Online-to-Batch Conversion

In this work, we give generalization bounds of statistical learning algorithms trained on samples drawn from a dependent data source, both in expectation and with high probability, using the Online-to-Batch conversion paradigm. We show that the generalization error of statistical learners in the dependent data setting is equivalent to the generalization error of statistical learners in the i.i.d. setting up to a term that depends on the decay rate of the underlying mixing stochastic process and is independent of the complexity of the statistical learner. Our proof techniques involve defining a new notion of stability of online learning algorithms based on Wasserstein distances and employing "near-martingale" concentration bounds for dependent random variables to arrive at appropriate upper bounds for the generalization error of statistical learners trained on dependent data.

Approximating Probability Distributions by ReLU Networks

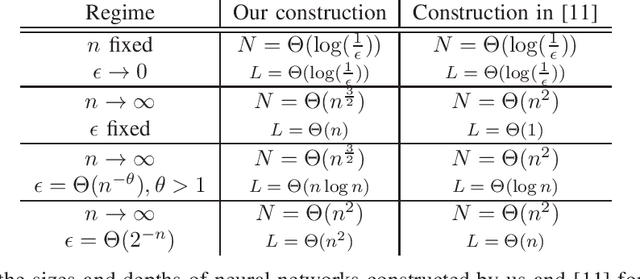
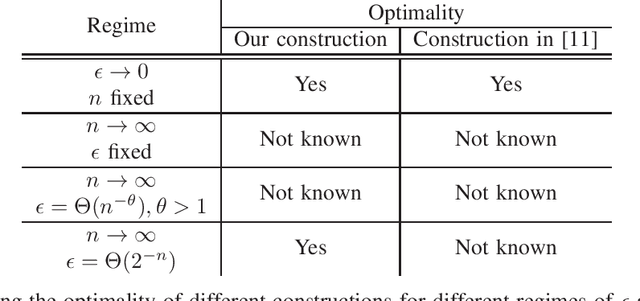
How many neurons are needed to approximate a target probability distribution using a neural network with a given input distribution and approximation error? This paper examines this question for the case when the input distribution is uniform, and the target distribution belongs to the class of histogram distributions. We obtain a new upper bound on the number of required neurons, which is strictly better than previously existing upper bounds. The key ingredient in this improvement is an efficient construction of the neural nets representing piecewise linear functions. We also obtain a lower bound on the minimum number of neurons needed to approximate the histogram distributions.