Approximating Probability Distributions by ReLU Networks
Paper and Code
Jan 25, 2021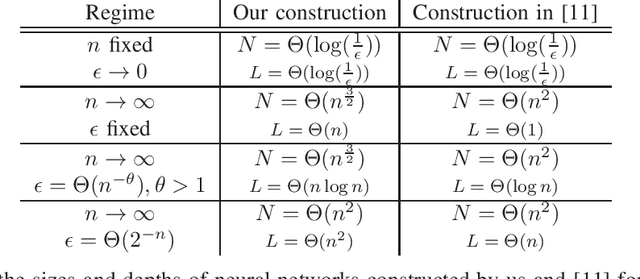
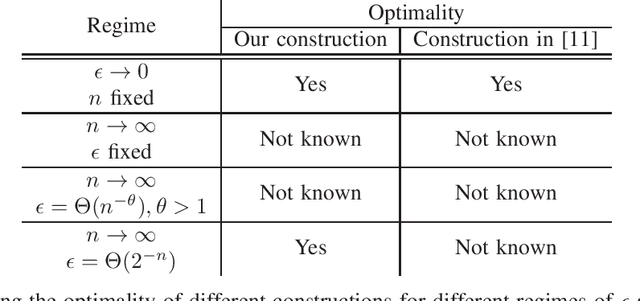
How many neurons are needed to approximate a target probability distribution using a neural network with a given input distribution and approximation error? This paper examines this question for the case when the input distribution is uniform, and the target distribution belongs to the class of histogram distributions. We obtain a new upper bound on the number of required neurons, which is strictly better than previously existing upper bounds. The key ingredient in this improvement is an efficient construction of the neural nets representing piecewise linear functions. We also obtain a lower bound on the minimum number of neurons needed to approximate the histogram distributions.
* Longer version of a paper accepted for presentation at the ITW 2020
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge