Multifidelity Cross-validation

Emulating the mapping between quantities of interest and their control parameters using surrogate models finds widespread application in engineering design, including in numerical optimization and uncertainty quantification. Gaussian process models can serve as a probabilistic surrogate model of unknown functions, thereby making them highly suitable for engineering design and decision-making in the presence of uncertainty. In this work, we are interested in emulating quantities of interest observed from models of a system at multiple fidelities, which trade accuracy for computational efficiency. Using multifidelity Gaussian process models, to efficiently fuse models at multiple fidelities, we propose a novel method to actively learn the surrogate model via leave-one-out cross-validation (LOO-CV). Our proposed multifidelity cross-validation (\texttt{MFCV}) approach develops an adaptive approach to reduce the LOO-CV error at the target (highest) fidelity, by learning the correlations between the LOO-CV at all fidelities. \texttt{MFCV} develops a two-step lookahead policy to select optimal input-fidelity pairs, both in sequence and in batches, both for continuous and discrete fidelity spaces. We demonstrate the utility of our method on several synthetic test problems as well as on the thermal stress analysis of a gas turbine blade.

qPOTS: Efficient batch multiobjective Bayesian optimization via Pareto optimal Thompson sampling

Classical evolutionary approaches for multiobjective optimization are quite effective but incur a lot of queries to the objectives; this can be prohibitive when objectives are expensive oracles. A sample-efficient approach to solving multiobjective optimization is via Gaussian process (GP) surrogates and Bayesian optimization (BO). Multiobjective Bayesian optimization (MOBO) involves the construction of an acquisition function which is optimized to acquire new observation candidates. This ``inner'' optimization can be hard due to various reasons: acquisition functions being nonconvex, nondifferentiable and/or unavailable in analytical form; the success of MOBO heavily relies on this inner optimization. We do away with this hard acquisition function optimization step and propose a simple, but effective, Thompson sampling based approach ($q\texttt{POTS}$) where new candidate(s) are chosen from the Pareto frontier of random GP posterior sample paths obtained by solving a much cheaper multiobjective optimization problem. To further improve computational tractability in higher dimensions we propose an automated active set of candidates selection combined with a Nystr\"{o}m approximation. Our approach applies to arbitrary GP prior assumptions and demonstrates strong empirical performance over the state of the art, both in terms of accuracy and computational efficiency, on synthetic as well as real-world experiments.

Data-Driven Wind Turbine Wake Modeling via Probabilistic Machine Learning

Wind farm design primarily depends on the variability of the wind turbine wake flows to the atmospheric wind conditions, and the interaction between wakes. Physics-based models that capture the wake flow-field with high-fidelity are computationally very expensive to perform layout optimization of wind farms, and, thus, data-driven reduced order models can represent an efficient alternative for simulating wind farms. In this work, we use real-world light detection and ranging (LiDAR) measurements of wind-turbine wakes to construct predictive surrogate models using machine learning. Specifically, we first demonstrate the use of deep autoencoders to find a low-dimensional \emph{latent} space that gives a computationally tractable approximation of the wake LiDAR measurements. Then, we learn the mapping between the parameter space and the (latent space) wake flow-fields using a deep neural network. Additionally, we also demonstrate the use of a probabilistic machine learning technique, namely, Gaussian process modeling, to learn the parameter-space-latent-space mapping in addition to the epistemic and aleatoric uncertainty in the data. Finally, to cope with training large datasets, we demonstrate the use of variational Gaussian process models that provide a tractable alternative to the conventional Gaussian process models for large datasets. Furthermore, we introduce the use of active learning to adaptively build and improve a conventional Gaussian process model predictive capability. Overall, we find that our approach provides accurate approximations of the wind-turbine wake flow field that can be queried at an orders-of-magnitude cheaper cost than those generated with high-fidelity physics-based simulations.

Enhanced data efficiency using deep neural networks and Gaussian processes for aerodynamic design optimization

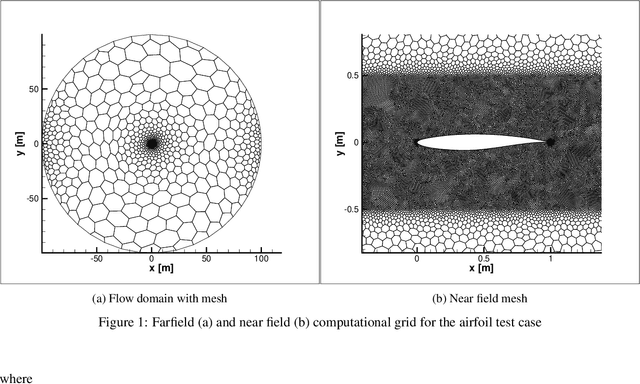
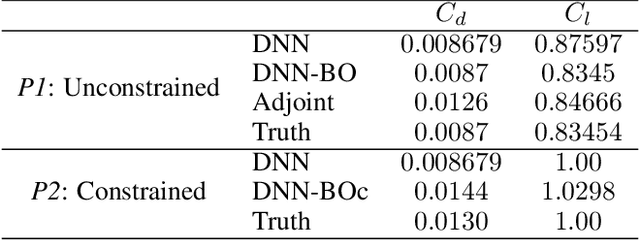
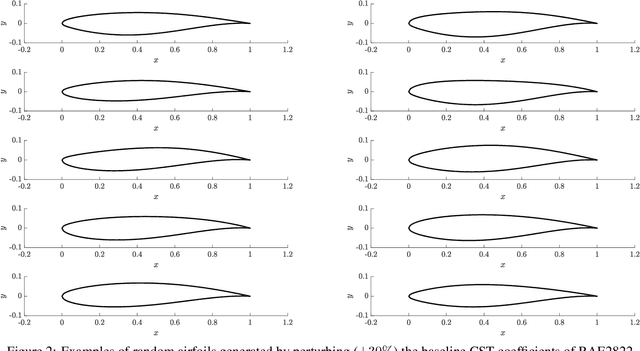
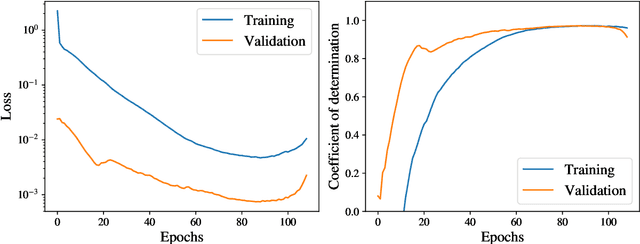
Adjoint-based optimization methods are attractive for aerodynamic shape design primarily due to their computational costs being independent of the dimensionality of the input space and their ability to generate high-fidelity gradients that can then be used in a gradient-based optimizer. This makes them very well suited for high-fidelity simulation based aerodynamic shape optimization of highly parametrized geometries such as aircraft wings. However, the development of adjoint-based solvers involve careful mathematical treatment and their implementation require detailed software development. Furthermore, they can become prohibitively expensive when multiple optimization problems are being solved, each requiring multiple restarts to circumvent local optima. In this work, we propose a machine learning enabled, surrogate-based framework that replaces the expensive adjoint solver, without compromising on predicting predictive accuracy. Specifically, we first train a deep neural network (DNN) from training data generated from evaluating the high-fidelity simulation model on a model-agnostic, design of experiments on the geometry shape parameters. The optimum shape may then be computed by using a gradient-based optimizer coupled with the trained DNN. Subsequently, we also perform a gradient-free Bayesian optimization, where the trained DNN is used as the prior mean. We observe that the latter framework (DNN-BO) improves upon the DNN-only based optimization strategy for the same computational cost. Overall, this framework predicts the true optimum with very high accuracy, while requiring far fewer high-fidelity function calls compared to the adjoint-based method. Furthermore, we show that multiple optimization problems can be solved with the same machine learning model with high accuracy, to amortize the offline costs associated with constructing our models.

Recursive Two-Step Lookahead Expected Payoff for Time-Dependent Bayesian Optimization

We propose a novel Bayesian method to solve the maximization of a time-dependent expensive-to-evaluate oracle. We are interested in the decision that maximizes the oracle at a finite time horizon, when relatively few noisy evaluations can be performed before the horizon. Our recursive, two-step lookahead expected payoff ($\texttt{r2LEY}$) acquisition function makes nonmyopic decisions at every stage by maximizing the estimated expected value of the oracle at the horizon. $\texttt{r2LEY}$ circumvents the evaluation of the expensive multistep (more than two steps) lookahead acquisition function by recursively optimizing a two-step lookahead acquisition function at every stage; unbiased estimators of this latter function and its gradient are utilized for efficient optimization. $\texttt{r2LEY}$ is shown to exhibit natural exploration properties far from the time horizon, enabling accurate emulation of the oracle, which is exploited in the final decision made at the horizon. To demonstrate the utility of $\texttt{r2LEY}$, we compare it with time-dependent extensions of popular myopic acquisition functions via both synthetic and real-world datasets.

Aerodynamic Data Fusion Towards the Digital Twin Paradigm

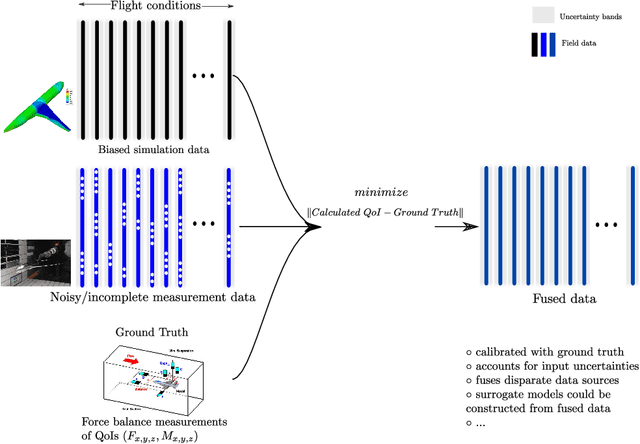
We consider the fusion of two aerodynamic data sets originating from differing fidelity physical or computer experiments. We specifically address the fusion of: 1) noisy and in-complete fields from wind tunnel measurements and 2) deterministic but biased fields from numerical simulations. These two data sources are fused in order to estimate the \emph{true} field that best matches measured quantities that serves as the ground truth. For example, two sources of pressure fields about an aircraft are fused based on measured forces and moments from a wind-tunnel experiment. A fundamental challenge in this problem is that the true field is unknown and can not be estimated with 100\% certainty. We employ a Bayesian framework to infer the true fields conditioned on measured quantities of interest; essentially we perform a \emph{statistical correction} to the data. The fused data may then be used to construct more accurate surrogate models suitable for early stages of aerospace design. We also introduce an extension of the Proper Orthogonal Decomposition with constraints to solve the same problem. Both methods are demonstrated on fusing the pressure distributions for flow past the RAE2822 airfoil and the Common Research Model wing at transonic conditions. Comparison of both methods reveal that the Bayesian method is more robust when data is scarce while capable of also accounting for uncertainties in the data. Furthermore, given adequate data, the POD based and Bayesian approaches lead to \emph{similar} results.