Aerodynamic Data Fusion Towards the Digital Twin Paradigm
Paper and Code
Nov 02, 2019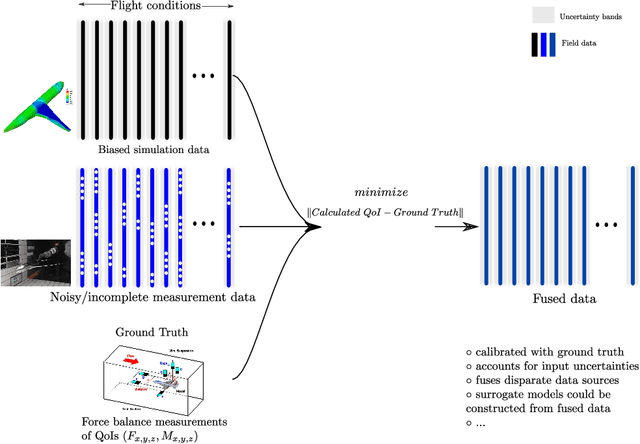



We consider the fusion of two aerodynamic data sets originating from differing fidelity physical or computer experiments. We specifically address the fusion of: 1) noisy and in-complete fields from wind tunnel measurements and 2) deterministic but biased fields from numerical simulations. These two data sources are fused in order to estimate the \emph{true} field that best matches measured quantities that serves as the ground truth. For example, two sources of pressure fields about an aircraft are fused based on measured forces and moments from a wind-tunnel experiment. A fundamental challenge in this problem is that the true field is unknown and can not be estimated with 100\% certainty. We employ a Bayesian framework to infer the true fields conditioned on measured quantities of interest; essentially we perform a \emph{statistical correction} to the data. The fused data may then be used to construct more accurate surrogate models suitable for early stages of aerospace design. We also introduce an extension of the Proper Orthogonal Decomposition with constraints to solve the same problem. Both methods are demonstrated on fusing the pressure distributions for flow past the RAE2822 airfoil and the Common Research Model wing at transonic conditions. Comparison of both methods reveal that the Bayesian method is more robust when data is scarce while capable of also accounting for uncertainties in the data. Furthermore, given adequate data, the POD based and Bayesian approaches lead to \emph{similar} results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge