A study on Ensemble Learning for Time Series Forecasting and the need for Meta-Learning

The contribution of this work is twofold: (1) We introduce a collection of ensemble methods for time series forecasting to combine predictions from base models. We demonstrate insights on the power of ensemble learning for forecasting, showing experiment results on about 16000 openly available datasets, from M4, M5, M3 competitions, as well as FRED (Federal Reserve Economic Data) datasets. Whereas experiments show that ensembles provide a benefit on forecasting results, there is no clear winning ensemble strategy (plus hyperparameter configuration). Thus, in addition, (2), we propose a meta-learning step to choose, for each dataset, the most appropriate ensemble method and their hyperparameter configuration to run based on dataset meta-features.

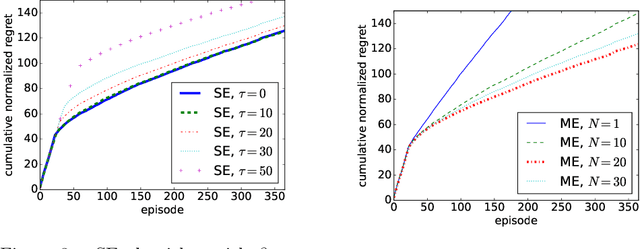
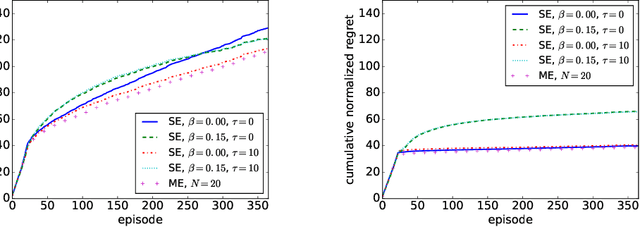
The Combinatorial Multi-Bandit Problem and its Application to Energy Management

We study a Combinatorial Multi-Bandit Problem motivated by applications in energy systems management. Given multiple probabilistic multi-arm bandits with unknown outcome distributions, the task is to optimize the value of a combinatorial objective function mapping the vector of individual bandit outcomes to a single scalar reward. Unlike in single-bandit problems with multi-dimensional action space, the outcomes of the individual bandits are observable in our setting and the objective function is known. Guided by the hypothesis that individual observability enables better trade-offs between exploration and exploitation, we generalize the lower regret bound for single bandits, showing that indeed for multiple bandits it admits parallelized exploration. For our energy management application we propose a range of algorithms that combine exploration principles for multi-arm bandits with mathematical programming. In an experimental study we demonstrate the effectiveness of our approach to learn action assignments for 150 bandits, each having 24 actions, within a horizon of 365 episodes.

HAMLET -- A Learning Curve-Enabled Multi-Armed Bandit for Algorithm Selection

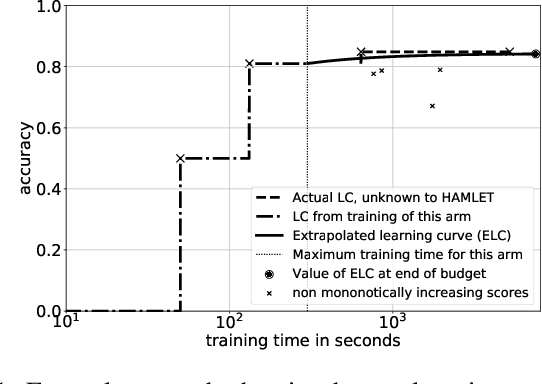
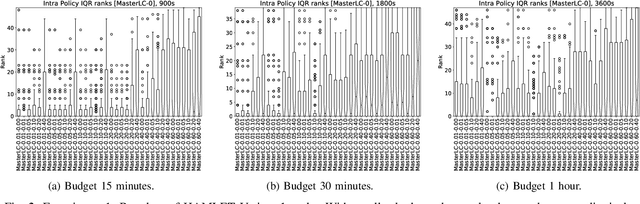
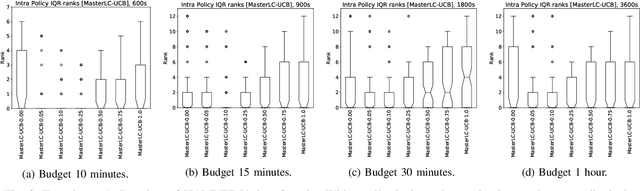
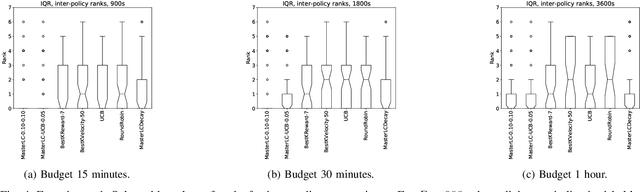
Automated algorithm selection and hyperparameter tuning facilitates the application of machine learning. Traditional multi-armed bandit strategies look to the history of observed rewards to identify the most promising arms for optimizing expected total reward in the long run. When considering limited time budgets and computational resources, this backward view of rewards is inappropriate as the bandit should look into the future for anticipating the highest final reward at the end of a specified time budget. This work addresses that insight by introducing HAMLET, which extends the bandit approach with learning curve extrapolation and computation time-awareness for selecting among a set of machine learning algorithms. Results show that the HAMLET Variants 1-3 exhibit equal or better performance than other bandit-based algorithm selection strategies in experiments with recorded hyperparameter tuning traces for the majority of considered time budgets. The best performing HAMLET Variant 3 combines learning curve extrapolation with the well-known upper confidence bound exploration bonus. That variant performs better than all non-HAMLET policies with statistical significance at the 95% level for 1,485 runs.