Scardina: Scalable Join Cardinality Estimation by Multiple Density Estimators

In recent years, machine learning-based cardinality estimation methods are replacing traditional methods. This change is expected to contribute to one of the most important applications of cardinality estimation, the query optimizer, to speed up query processing. However, none of the existing methods do not precisely estimate cardinalities when relational schemas consist of many tables with strong correlations between tables/attributes. This paper describes that multiple density estimators can be combined to effectively target the cardinality estimation of data with large and complex schemas having strong correlations. We propose Scardina, a new join cardinality estimation method using multiple partitioned models based on the schema structure.

Scaling Private Deep Learning with Low-Rank and Sparse Gradients

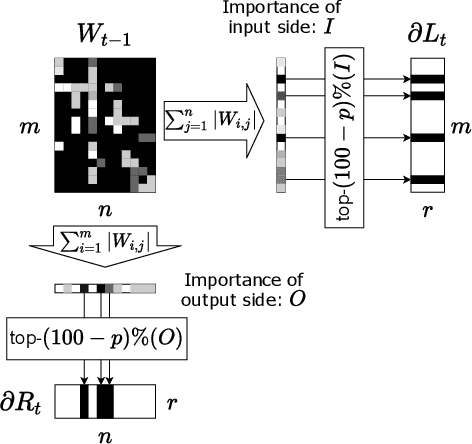
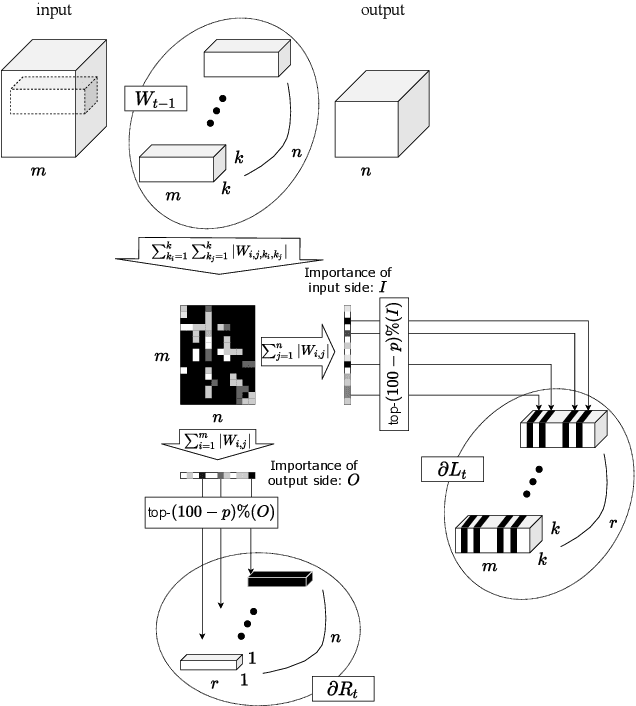
Applying Differentially Private Stochastic Gradient Descent (DPSGD) to training modern, large-scale neural networks such as transformer-based models is a challenging task, as the magnitude of noise added to the gradients at each iteration scales with model dimension, hindering the learning capability significantly. We propose a unified framework, $\textsf{LSG}$, that fully exploits the low-rank and sparse structure of neural networks to reduce the dimension of gradient updates, and hence alleviate the negative impacts of DPSGD. The gradient updates are first approximated with a pair of low-rank matrices. Then, a novel strategy is utilized to sparsify the gradients, resulting in low-dimensional, less noisy updates that are yet capable of retaining the performance of neural networks. Empirical evaluation on natural language processing and computer vision tasks shows that our method outperforms other state-of-the-art baselines.