Scaling Private Deep Learning with Low-Rank and Sparse Gradients
Paper and Code
Jul 06, 2022

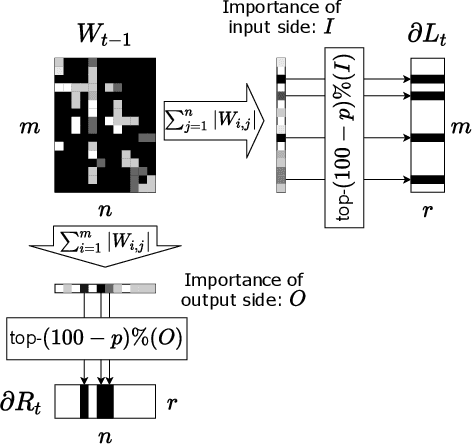
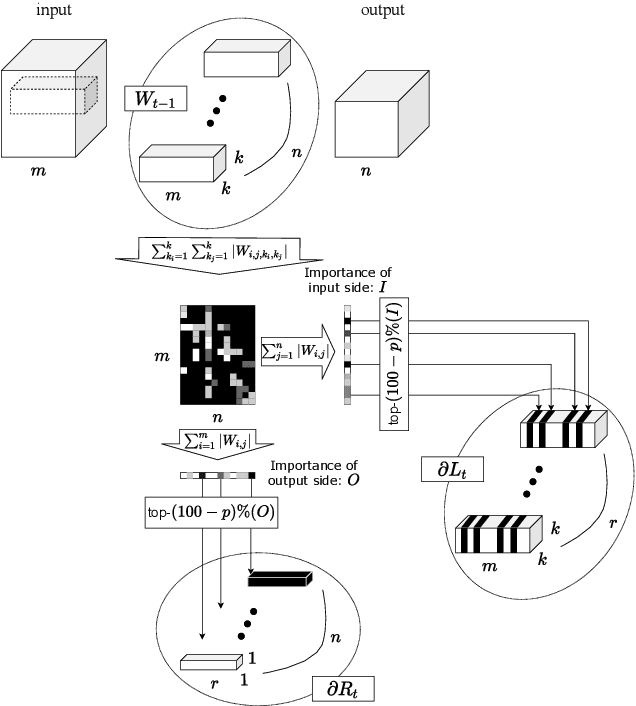
Applying Differentially Private Stochastic Gradient Descent (DPSGD) to training modern, large-scale neural networks such as transformer-based models is a challenging task, as the magnitude of noise added to the gradients at each iteration scales with model dimension, hindering the learning capability significantly. We propose a unified framework, $\textsf{LSG}$, that fully exploits the low-rank and sparse structure of neural networks to reduce the dimension of gradient updates, and hence alleviate the negative impacts of DPSGD. The gradient updates are first approximated with a pair of low-rank matrices. Then, a novel strategy is utilized to sparsify the gradients, resulting in low-dimensional, less noisy updates that are yet capable of retaining the performance of neural networks. Empirical evaluation on natural language processing and computer vision tasks shows that our method outperforms other state-of-the-art baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge