Valid and Exact Statistical Inference for Multi-dimensional Multiple Change-Points by Selective Inference

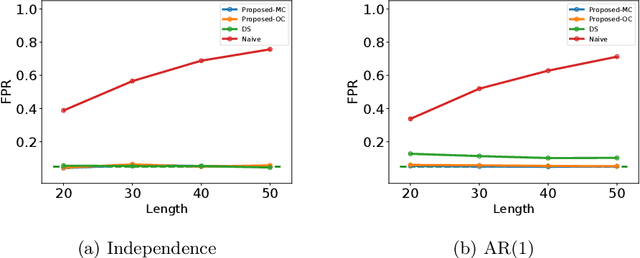
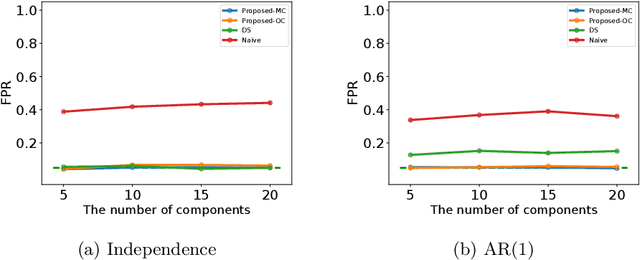
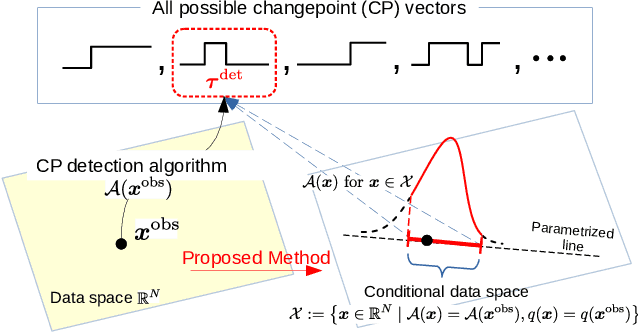
In this paper, we study statistical inference of change-points (CPs) in multi-dimensional sequence. In CP detection from a multi-dimensional sequence, it is often desirable not only to detect the location, but also to identify the subset of the components in which the change occurs. Several algorithms have been proposed for such problems, but no valid exact inference method has been established to evaluate the statistical reliability of the detected locations and components. In this study, we propose a method that can guarantee the statistical reliability of both the location and the components of the detected changes. We demonstrate the effectiveness of the proposed method by applying it to the problems of genomic abnormality identification and human behavior analysis.

Computing Valid p-value for Optimal Changepoint by Selective Inference using Dynamic Programming

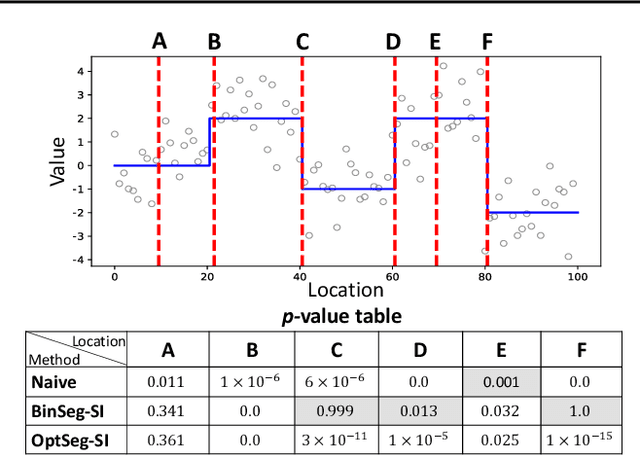
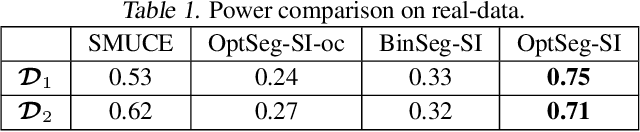
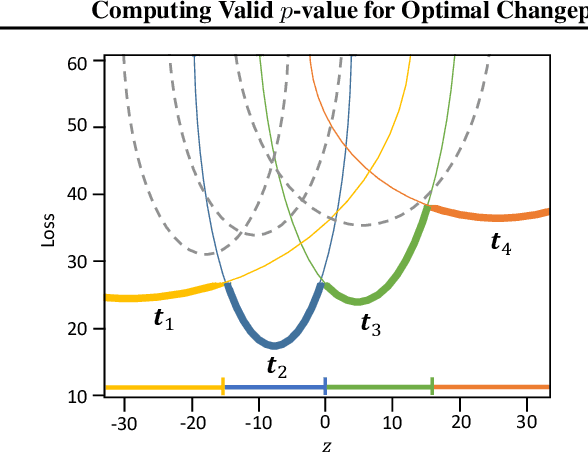
There is a vast body of literature related to methods for detecting changepoints (CP). However, less attention has been paid to assessing the statistical reliability of the detected CPs. In this paper, we introduce a novel method to perform statistical inference on the significance of the CPs, estimated by a Dynamic Programming (DP)-based optimal CP detection algorithm. Based on the selective inference (SI) framework, we propose an exact (non-asymptotic) approach to compute valid p-values for testing the significance of the CPs. Although it is well-known that SI has low statistical power because of over-conditioning, we address this disadvantage by introducing parametric programming techniques. Then, we propose an efficient method to conduct SI with the minimum amount of conditioning, leading to high statistical power. We conduct experiments on both synthetic and real-world datasets, through which we offer evidence that our proposed method is more powerful than existing methods, has decent performance in terms of computational efficiency, and provides good results in many practical applications.