Computing Valid p-value for Optimal Changepoint by Selective Inference using Dynamic Programming
Paper and Code
Feb 21, 2020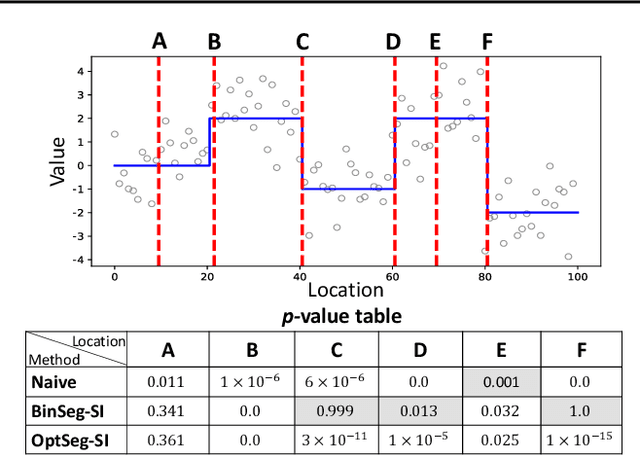
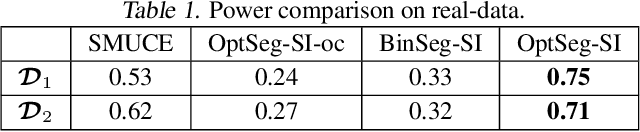
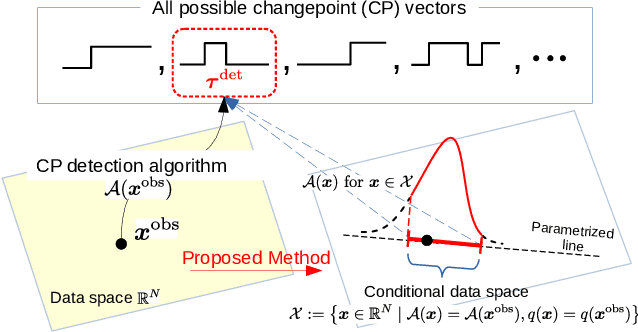
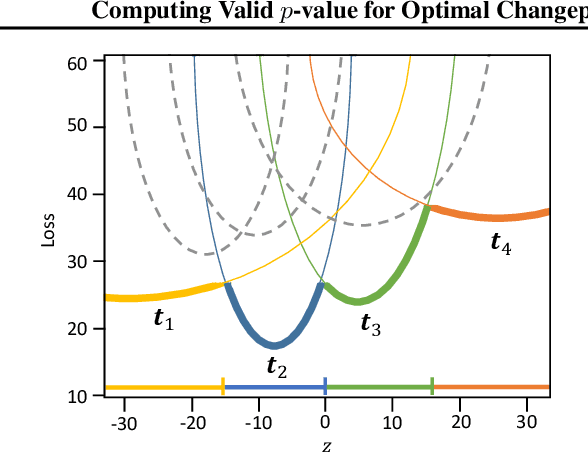
There is a vast body of literature related to methods for detecting changepoints (CP). However, less attention has been paid to assessing the statistical reliability of the detected CPs. In this paper, we introduce a novel method to perform statistical inference on the significance of the CPs, estimated by a Dynamic Programming (DP)-based optimal CP detection algorithm. Based on the selective inference (SI) framework, we propose an exact (non-asymptotic) approach to compute valid p-values for testing the significance of the CPs. Although it is well-known that SI has low statistical power because of over-conditioning, we address this disadvantage by introducing parametric programming techniques. Then, we propose an efficient method to conduct SI with the minimum amount of conditioning, leading to high statistical power. We conduct experiments on both synthetic and real-world datasets, through which we offer evidence that our proposed method is more powerful than existing methods, has decent performance in terms of computational efficiency, and provides good results in many practical applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge