Min-Max Optimization Made Simple: Approximating the Proximal Point Method via Contraction Maps

In this paper we present a first-order method that admits near-optimal convergence rates for convex/concave min-max problems while requiring a simple and intuitive analysis. Similarly to the seminal work of Nemirovski and the recent approach of Piliouras et al. in normal form games, our work is based on the fact that the update rule of the Proximal Point method (PP) can be approximated up to accuracy $\epsilon$ with only $O(\log 1/\epsilon)$ additional gradient-calls through the iterations of a contraction map. Then combining the analysis of (PP) method with an error-propagation analysis we establish that the resulting first order method, called Clairvoyant Extra Gradient, admits near-optimal time-average convergence for general domains and last-iterate convergence in the unconstrained case.

Fast Convergence of Optimistic Gradient Ascent in Network Zero-Sum Extensive Form Games

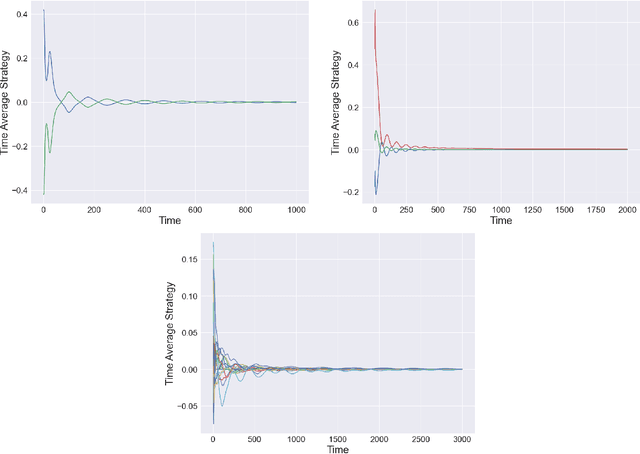
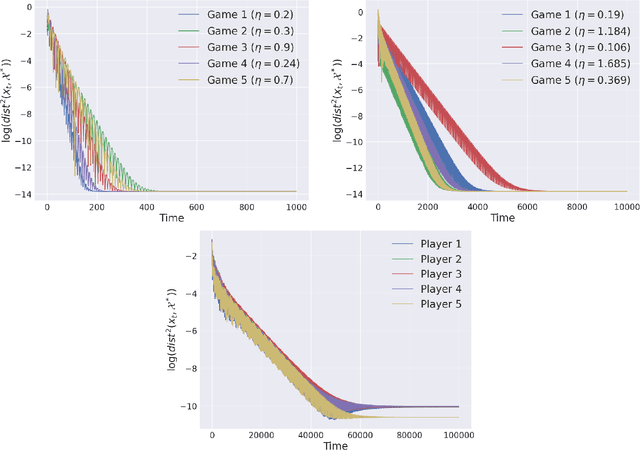
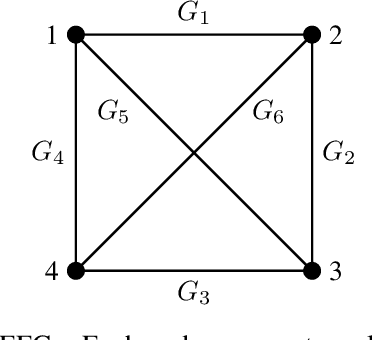
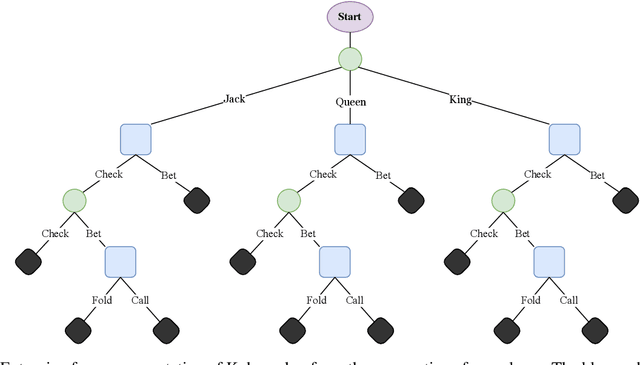
The study of learning in games has thus far focused primarily on normal form games. In contrast, our understanding of learning in extensive form games (EFGs) and particularly in EFGs with many agents lags far behind, despite them being closer in nature to many real world applications. We consider the natural class of Network Zero-Sum Extensive Form Games, which combines the global zero-sum property of agent payoffs, the efficient representation of graphical games as well the expressive power of EFGs. We examine the convergence properties of Optimistic Gradient Ascent (OGA) in these games. We prove that the time-average behavior of such online learning dynamics exhibits $O(1/T)$ rate convergence to the set of Nash Equilibria. Moreover, we show that the day-to-day behavior also converges to Nash with rate $O(c^{-t})$ for some game-dependent constant $c>0$.

Optimal No-Regret Learning in General Games: Bounded Regret with Unbounded Step-Sizes via Clairvoyant MWU

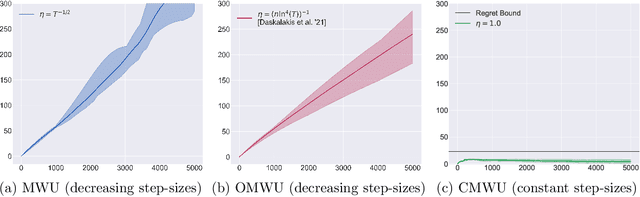
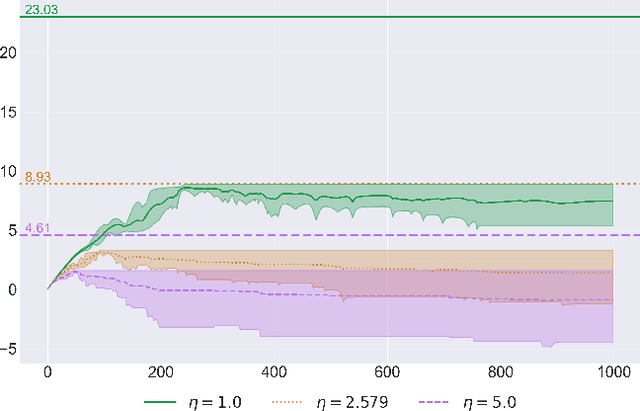
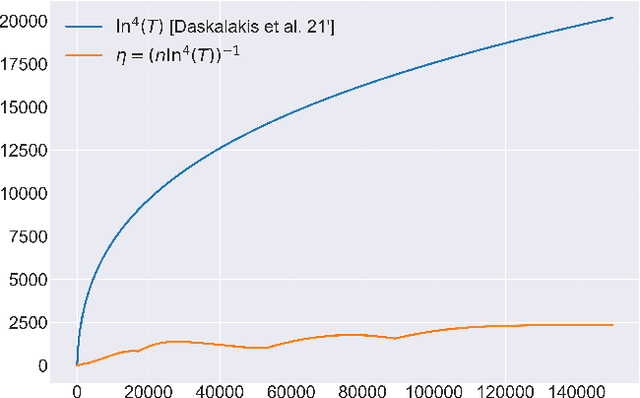
In this paper we solve the problem of no-regret learning in general games. Specifically, we provide a simple and practical algorithm that achieves constant regret with fixed step-sizes. The cumulative regret of our algorithm provably decreases linearly as the step-size increases. Our findings depart from the prevailing paradigm that vanishing step-sizes are a prerequisite for low regret as championed by all state-of-the-art methods to date. We shift away from this paradigm by defining a novel algorithm that we call Clairvoyant Multiplicative Weights Updates (CMWU). CMWU is Multiplicative Weights Updates (MWU) equipped with a mental model (jointly shared across all agents) about the state of the system in its next period. Each agent records its mixed strategy, i.e., its belief about what it expects to play in the next period, in this shared mental model which is internally updated using MWU without any changes to the real-world behavior up until it equilibrates, thus marking its consistency with the next day's real-world outcome. It is then and only then that agents take action in the real-world, effectively doing so with the "full knowledge" of the state of the system on the next day, i.e., they are clairvoyant. CMWU effectively acts as MWU with one day look-ahead, achieving bounded regret. At a technical level, we establish that self-consistent mental models exist for any choice of step-sizes and provide bounds on the step-size under which their uniqueness and linear-time computation are guaranteed via contraction mapping arguments. Our arguments extend well beyond normal-form games with little effort.

Online Learning in Periodic Zero-Sum Games

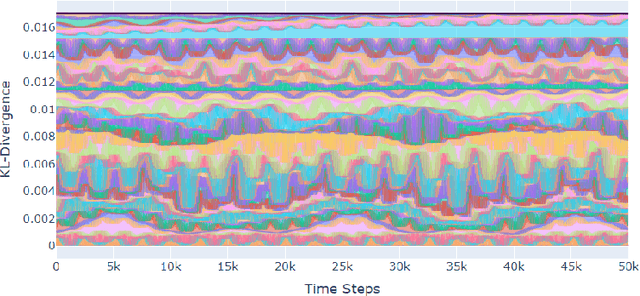
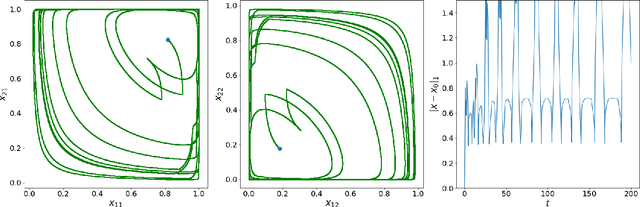
A seminal result in game theory is von Neumann's minmax theorem, which states that zero-sum games admit an essentially unique equilibrium solution. Classical learning results build on this theorem to show that online no-regret dynamics converge to an equilibrium in a time-average sense in zero-sum games. In the past several years, a key research direction has focused on characterizing the day-to-day behavior of such dynamics. General results in this direction show that broad classes of online learning dynamics are cyclic, and formally Poincar\'{e} recurrent, in zero-sum games. We analyze the robustness of these online learning behaviors in the case of periodic zero-sum games with a time-invariant equilibrium. This model generalizes the usual repeated game formulation while also being a realistic and natural model of a repeated competition between players that depends on exogenous environmental variations such as time-of-day effects, week-to-week trends, and seasonality. Interestingly, time-average convergence may fail even in the simplest such settings, in spite of the equilibrium being fixed. In contrast, using novel analysis methods, we show that Poincar\'{e} recurrence provably generalizes despite the complex, non-autonomous nature of these dynamical systems.

Evolutionary Game Theory Squared: Evolving Agents in Endogenously Evolving Zero-Sum Games

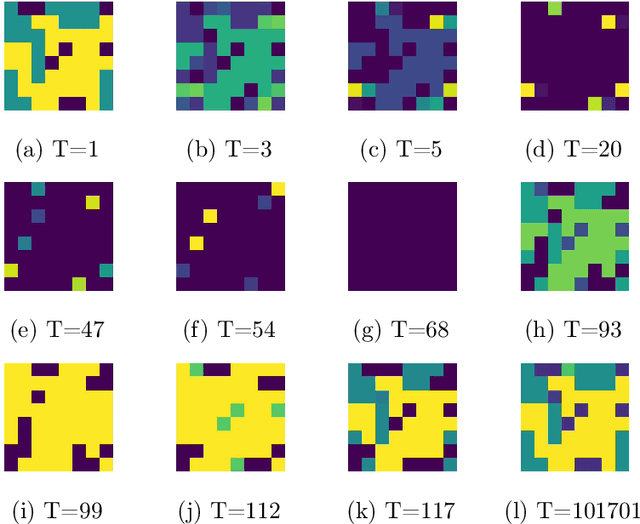
The predominant paradigm in evolutionary game theory and more generally online learning in games is based on a clear distinction between a population of dynamic agents that interact given a fixed, static game. In this paper, we move away from the artificial divide between dynamic agents and static games, to introduce and analyze a large class of competitive settings where both the agents and the games they play evolve strategically over time. We focus on arguably the most archetypal game-theoretic setting -- zero-sum games (as well as network generalizations) -- and the most studied evolutionary learning dynamic -- replicator, the continuous-time analogue of multiplicative weights. Populations of agents compete against each other in a zero-sum competition that itself evolves adversarially to the current population mixture. Remarkably, despite the chaotic coevolution of agents and games, we prove that the system exhibits a number of regularities. First, the system has conservation laws of an information-theoretic flavor that couple the behavior of all agents and games. Secondly, the system is Poincar\'{e} recurrent, with effectively all possible initializations of agents and games lying on recurrent orbits that come arbitrarily close to their initial conditions infinitely often. Thirdly, the time-average agent behavior and utility converge to the Nash equilibrium values of the time-average game. Finally, we provide a polynomial time algorithm to efficiently predict this time-average behavior for any such coevolving network game.