Fast Convergence of Optimistic Gradient Ascent in Network Zero-Sum Extensive Form Games
Paper and Code
Jul 18, 2022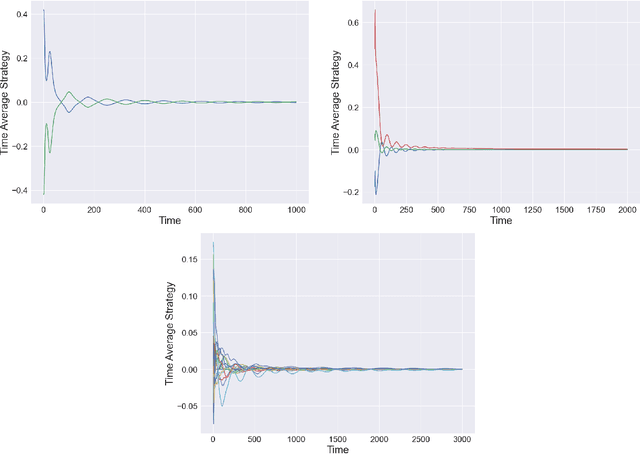
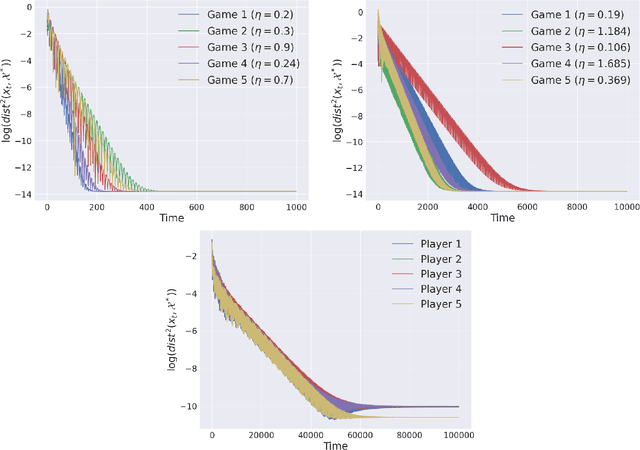
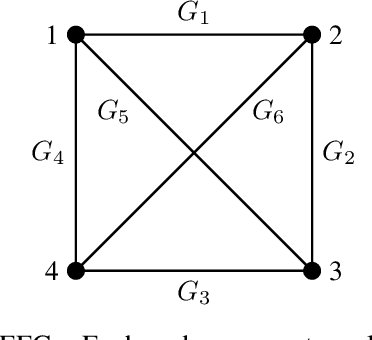
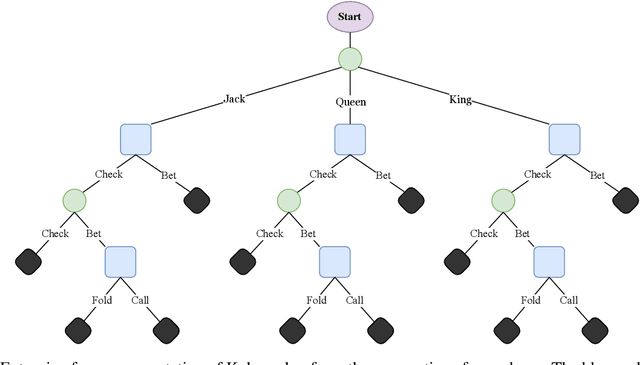
The study of learning in games has thus far focused primarily on normal form games. In contrast, our understanding of learning in extensive form games (EFGs) and particularly in EFGs with many agents lags far behind, despite them being closer in nature to many real world applications. We consider the natural class of Network Zero-Sum Extensive Form Games, which combines the global zero-sum property of agent payoffs, the efficient representation of graphical games as well the expressive power of EFGs. We examine the convergence properties of Optimistic Gradient Ascent (OGA) in these games. We prove that the time-average behavior of such online learning dynamics exhibits $O(1/T)$ rate convergence to the set of Nash Equilibria. Moreover, we show that the day-to-day behavior also converges to Nash with rate $O(c^{-t})$ for some game-dependent constant $c>0$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge