Ryan R. Strauss
Any Variational Autoencoder Can Do Arbitrary Conditioning
Jan 28, 2022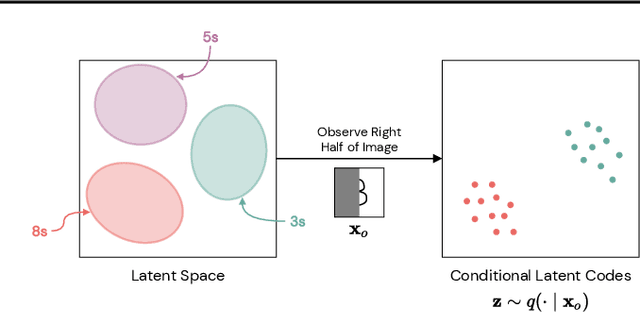

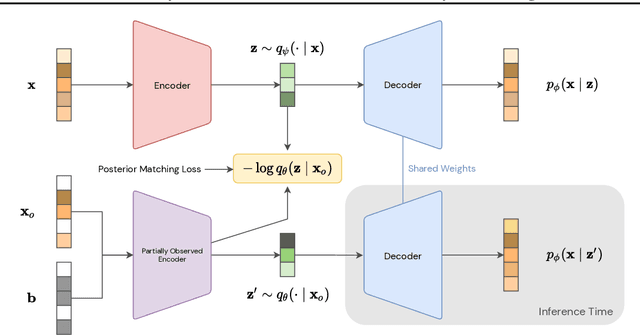

Abstract:Arbitrary conditioning is an important problem in unsupervised learning, where we seek to model the conditional densities $p(\mathbf{x}_u \mid \mathbf{x}_o)$ that underly some data, for all possible non-intersecting subsets $o, u \subset \{1, \dots , d\}$. However, the vast majority of density estimation only focuses on modeling the joint distribution $p(\mathbf{x})$, in which important conditional dependencies between features are opaque. We propose a simple and general framework, coined Posterior Matching, that enables any Variational Autoencoder (VAE) to perform arbitrary conditioning, without modification to the VAE itself. Posterior Matching applies to the numerous existing VAE-based approaches to joint density estimation, thereby circumventing the specialized models required by previous approaches to arbitrary conditioning. We find that Posterior Matching achieves performance that is comparable or superior to current state-of-the-art methods for a variety of tasks.
Arbitrary Conditional Distributions with Energy
Feb 08, 2021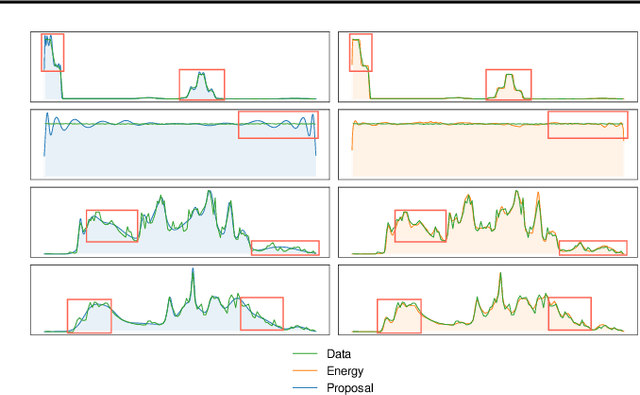


Abstract:Modeling distributions of covariates, or density estimation, is a core challenge in unsupervised learning. However, the majority of work only considers the joint distribution, which has limited relevance to practical situations. A more general and useful problem is arbitrary conditional density estimation, which aims to model any possible conditional distribution over a set of covariates, reflecting the more realistic setting of inference based on prior knowledge. We propose a novel method, Arbitrary Conditioning with Energy (ACE), that can simultaneously estimate the distribution $p(\mathbf{x}_u \mid \mathbf{x}_o)$ for all possible subsets of features $\mathbf{x}_u$ and $\mathbf{x}_o$. ACE uses an energy function to specify densities, bypassing the architectural restrictions imposed by alternative methods and the biases imposed by tractable parametric distributions. We also simplify the learning problem by only learning one-dimensional conditionals, from which more complex distributions can be recovered during inference. Empirically, we show that ACE achieves state-of-the-art for arbitrary conditional and marginal likelihood estimation and for tabular data imputation.
Unsupervised Learning for Identifying Events in Active Target Experiments
Aug 07, 2020Abstract:This article presents novel applications of unsupervised machine learning methods to the problem of event separation in an active target detector, the Active-Target Time Projection Chamber (AT-TPC). The overarching goal is to group similar events in the early stages of the data analysis, thereby improving efficiency by limiting the computationally expensive processing of unnecessary events. The application of unsupervised clustering algorithms to the analysis of two-dimensional projections of particle tracks from a resonant proton scattering experiment on $^{46}$Ar is introduced. We explore the performance of autoencoder neural networks and a pre-trained VGG16 convolutional neural network. We find that a $K$-means algorithm applied to the simulated data in the VGG16 latent space forms almost perfect clusters. Additionally, the VGG16+$K$-means approach finds high purity clusters of proton events for real experimental data. We also explore the application of clustering the latent space of autoencoder neural networks for event separation. While these networks show strong performance, they suffer from high variability in their results.
Machine Learning Methods for Track Classification in the AT-TPC
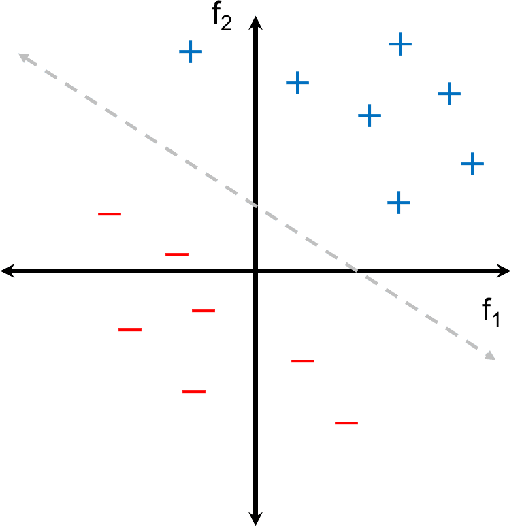
Oct 21, 2018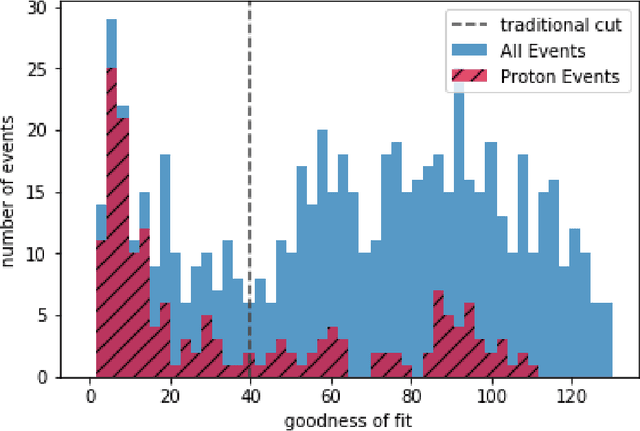

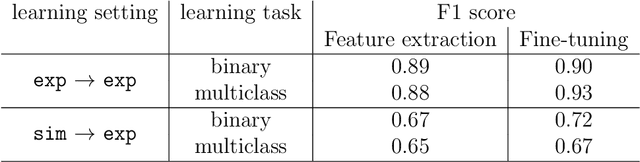
Abstract:We evaluate machine learning methods for event classification in the Active-Target Time Projection Chamber detector at the National Superconducting Cyclotron Laboratory (NSCL) at Michigan State University. An automated method to single out the desired reaction product would result in more accurate physics results as well as a faster analysis process. Binary and multi-class classification methods were tested on data produced by the $^{46}$Ar(p,p) experiment run at the NSCL in September 2015. We found a Convolutional Neural Network to be the most successful classifier of proton scattering events for transfer learning. Results from this investigation and recommendations for event classification in future experiments are presented.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge