Parametric Matrix Models

We present a general class of machine learning algorithms called parametric matrix models. Parametric matrix models are based on matrix equations, and the design is motivated by the efficiency of reduced basis methods for approximating solutions of parametric equations. The dependent variables can be defined implicitly or explicitly, and the equations may use algebraic, differential, or integral relations. Parametric matrix models can be trained with empirical data only, and no high-fidelity model calculations are needed. While originally designed for scientific computing, parametric matrix models are universal function approximators that can be applied to general machine learning problems. After introducing the underlying theory, we apply parametric matrix models to a series of different challenges that show their performance for a wide range of problems. For all the challenges tested here, parametric matrix models produce accurate results within a computational framework that allows for parameter extrapolation and interpretability.

Artificial Intelligence and Machine Learning in Nuclear Physics

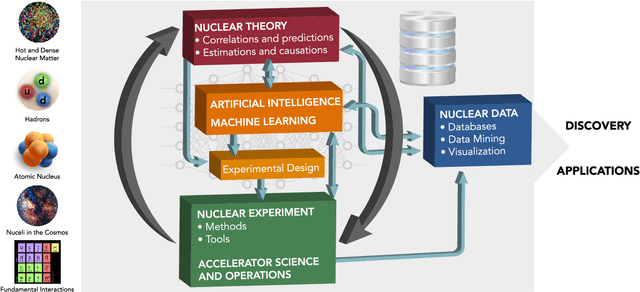
Advances in artificial intelligence/machine learning methods provide tools that have broad applicability in scientific research. These techniques are being applied across the diversity of nuclear physics research topics, leading to advances that will facilitate scientific discoveries and societal applications. This Review gives a snapshot of nuclear physics research which has been transformed by artificial intelligence and machine learning techniques.

Unsupervised Learning for Identifying Events in Active Target Experiments

This article presents novel applications of unsupervised machine learning methods to the problem of event separation in an active target detector, the Active-Target Time Projection Chamber (AT-TPC). The overarching goal is to group similar events in the early stages of the data analysis, thereby improving efficiency by limiting the computationally expensive processing of unnecessary events. The application of unsupervised clustering algorithms to the analysis of two-dimensional projections of particle tracks from a resonant proton scattering experiment on $^{46}$Ar is introduced. We explore the performance of autoencoder neural networks and a pre-trained VGG16 convolutional neural network. We find that a $K$-means algorithm applied to the simulated data in the VGG16 latent space forms almost perfect clusters. Additionally, the VGG16+$K$-means approach finds high purity clusters of proton events for real experimental data. We also explore the application of clustering the latent space of autoencoder neural networks for event separation. While these networks show strong performance, they suffer from high variability in their results.